Signal Processing Toolbox

離散コサイン変換

ツールボックスの関数dctは、入力ベクトルまたは行列の離散コサイン変換(DCT)を計算します。数学的には、入力データ列xのDCTは、つぎのように表されます。

ここで、つぎのようになります。

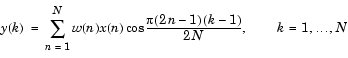
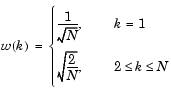
DCTは、離散フーリエ変換に密接に関連しています。DFTは、実際、データ列のDCT計算における1つのステップですが、DCTには望ましいエネルギー集中特性があり、数個の変換係数のみで列内のエネルギーの大部分を表現します。DCTのエネルギー集中特性は、データ通信などのアプリケーションに役立ちます。

関数idctは、入力列に対する逆DCTを計算し、DCT係数の全体、または、一部分から信号を復元します。逆離散コサイン変換は、つぎのようになります。

ここで、つぎのようになります。

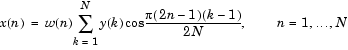
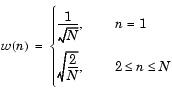
上述したエネルギー集中により、DCT係数の一部分のみから信号を復元することができます。たとえば、つぎのようにして、1000 Hzでサンプリングした25 Hzの正弦波列を作成します。

t = (0:1/999:1);
x = sin(2*pi*25*t);

このデータ列のDCTを計算し、53より大きい値(オリジナルの1000個のDCT係数のうちの12個)をもつ成分のみを用いて信号を復元します。

y = dct(x);               % DCTの計算
y2 = find(abs(y) < 53);   % 12個の係数を使用
y(y2) = zeros(size(y2));  % ゼロ出力点 < 53 
z = idct(y);              % 逆DCTを用いた信号の復元

つぎのようにして、オリジナルのデータ列と復元したデータ列をプロットします。

plot(t,x)
plot(t,z), axis([0 1 -1 1])

復元の精度の1つの尺度は、

norm(x-z)/norm(x)

すなわち、オリジナルの信号と復元した信号とのズレのノルムをオリジナルの信号のノルムで除算したものです。この場合では、復元の相対誤差は0.1443 です。復元された信号は、オリジナルの信号のエネルギーの約 85%を保持しています。

Chirp z-変換

Hilbert 変換