Signal Processing Toolbox

cohere

2つの信号間の2乗コヒーレンス関数の推定

表示

Cxy = cohere(x,y)
Cxy = cohere(x,y,nfft)
[Cxy,f] = cohere(x,y,nfft,fs)
Cxy = cohere(x,y,nfft,fs,window)
Cxy = cohere(x,y,nfft,fs,window,numoverlap)
Cxy = cohere(x,y,...,'dflag')
cohere(x,y)

詳細

Cxy = cohere(x,y) は、長さnの信号ベクトルxとyの間の2乗コヒーレンスを求めます。コヒーレンスは、xおよびyのパワースペクトルとxおよびyのクロススペクトルの関数で、つぎのように表されます。

xとyは、同じ長さでなければなりません。

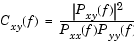
nfftは、cohereが使用するFFTの長さを設定します。この値により、コヒーレンスを計算する周波数を決定します。fsは、サンプリング周波数を設定するスカラ値です。windowは、cohereがxおよびyベクトルの分割に使用するウィンドウ関数とサンプル数を設定します。numoverlapは、分割したデータ間での重ね合わせを行なうサンプル数です。入力引数を省略すると、デフォルト値が使われます。

Cxy = cohere(x,y)は、つぎのデフォルト値を使用します。

• nfft = min(256,length(x))
• fs = 2
• window は、長さnfftの周期的な Hann (Hanning) ウインドウ
• numoverlap = 0

xが実数の場合、cohereは正の周波数のみでコヒーレンス関数を推定します。この場合、出力Cxyは、nfftが偶数の場合、長さ(nfft/2 + 1)の列ベクトル、nが奇数の場合、長さ(nfft + 1)/2の列ベクトルとなります。xまたはyが複素数の場合、cohereは正と負の周波数でコヒーレンス関数を推定し、Cxyの長さはnfftとなります。

Cxy = cohere(x,y,nfft) は、xに対するパワースペクトルの推定に長さnfftのFFTを使用します。実行速度を最も速くするには、nfftを2のベキ乗として設定します。

[Cxy,f] = cohere(x,y,nfft,fs) は、計算するコヒーレンスの周波数をベクトルfに出力します。fsは、サンプリング周波数です。fは、Cxyと同じ大きさなので、plot(f,Cxy)は、適切にスケーリングされた周波数に対するコヒーレンス関数をプロットします。fsは、周波数を求めるだけのもので、出力Cxyには影響しません。

cohere(x,y,nfft,fs,window) は、ベクトルxおよびyの分割したものに対するウィンドウ関数およびウインドウのサンプル数を設定します。windowにスカラ値を与えた場合、cohereは、その値を長さとするHannウィンドウを使用します。ウィンドウの長さは、nfft以下でなければなりません。ウィンドウの長さがnfftを越えていれば、cohereは、分割毎にゼロを付加します。

cohere(x,y,nfft,fs,window,numoverlap) は、numoverlapサンプルで、分割したxを重ね合わせます。

xまたはy以外のどの入力引数にも、空行列[]を使って、デフォルト値を設定することができます。たとえば、

cohere(x,y,[],[],kaiser(128,5));

は、 nfft の値として256を、 fs の値として2を、それぞれ使用します。

cohere(x,y,...,'dflag') は、トレンド除去オプションを設定します。ここで、dflag にはつぎの文字列を設定できます。

• linear：ウィンドウを適用する前にx、yから各々の最適近似直線を除去します。
• mean：ウィンドウを適用する前にx、yから各々の平均値を除去します。
• none：トレンド除去を行ないません(デフォルト)

引数dflagは、入力引数のリストの最後に付けなければなりません。cohereは、省略した入力引数の数に関係なく、dflag文字列を認識します。

cohere は、出力引数を設定しないと、周波数に対するコヒーレンス推定値をカレントのFigureウィンドウにプロットします。

例題

2つの有色雑音列xとyのコヒーレンス推定値を計算して、プロットします。

randn('state',0);
h = fir1(30,0.2,boxcar(31));
h1 = ones(1,10)/sqrt(10);
r = randn(16384,1);
x = filter(h1,1,r);
y = filter(h,1,x);
cohere(x,y,1024,[],[],512)

診断

誤った引数を使用した場合、つぎのような警告メッセージが表示されます。

Requires window's length to be no greater than the FFT length.
Requires NOVERLAP to be strictly less than the window length.
Requires positive integer values for NFFT and NOVERLAP.
Requires vector (either row or column) input.
Requires inputs X and Y to have the same length.

アルゴリズム

cohereは、つぎのように、パワースペクトル推定のWelch法(参考文献[2]および[3]を参照)を使って、2乗コヒーレンス関数(参考文献[1])を推定します。

1. 信号xおよびyを重ね合せを考慮して分割し、各分割データのトレンド除去を行い、その結果にwindowを適用します。
2. その結果に対して、長さnfftの高速フーリエ変換を計算します。
3. xのスペクトルの2乗を平均してPxxを作成し、yのスペクトルの2乗を平均してPyyを作成し、xとyのスペクトルの積を平均してPxyを作成します。そして、つぎのステートメントによりCxyを計算します。

   Cxy = abs(Pxy).^2/(Pxx.*Pyy)
   

参考

csd	2つの信号のクロススペクトル密度(CSD)の推定
pwelch	Welch法を使ったパワースペクトル密度(PSD)の推定
tfe	入力および出力からの伝達関数の推定

参考文献

[1] Kay, S.M. Modern Spectral Estimation. Englewood Cliffs, NJ: Prentice-Hall, 1988. Pg. 454.

[2] Rabiner, L.R., and B. Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975.

[3] Welch, P.D. "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms." IEEE Trans. Audio Electroacoust. Vol. AU-15 (June 1967). Pgs. 70-73.

chirp

conv