Control System Toolbox関数リファレンス

obsvf

可観測性ステアケース型を計算

表示

[Abar,Bbar,Cbar,T,k] = obsvf(A,B,C)
[Abar,Bbar,Cbar,T,k] = obsvf(A,B,C,tol)

詳細

(A,C)の可観測性行列のランクが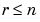の場合(nは、AAのサイズ)、つぎのような相似変換が存在します。

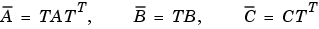
この場合、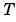はユニタリで、変換したシステムは、(存在すれば)左上隅に不可観測モードをもつステアケース型をもっています。

この場合、は可観測で、の固有値は不可観測モードです。

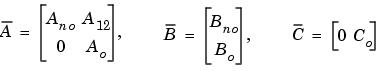
[Abar,Bbar,Cbar,T,k] = obsvf(A,B,C) は、行列A、B、 Cをもつ状態空間システムを上で説明した可観測性ステアケース型Abar、Bbar、Cbarに分解します。Tは相似変換行列で、kは長さnのベクトルです。この場合、nはAの状態数です。kの各成分は変換行列計算の各ステップで因数分解した可観測状態数を表しています[1]。kの中の非ゼロ要素の数はTを計算するために必要とされた繰り返し回数を示しており、sum(k) は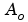の中の状態数、Abarの可観測部分です。

obsvf(A,B,C,tol) は、可観測/不可観測部分空間を計算するときにトレランスtol を使用します。トレランスを設定しないと、デフォルト10*n*norm(a,1)*epsが設定されます。

例題

つぎの可観測性ステアケース型を作成します。

A =
     1     1
     4    -2

B =
     1    -1
     1    -1

C =
     1     0
     0     1

つぎのように入力します。

[Abar,Bbar,Cbar,T,k] = obsvf(A,B,C)
Abar =
     1     1
     4    -2
Bbar =
     1     1
     1    -1
Cbar =
     1     0
     0     1
T =
     1     0
     0     1
k =
     2     0

アルゴリズム

obsvfは、ctrbfを呼び出し、双対性を用いることによって、[1]のステアケースアルゴリズムを実現するM-ファイルです。

参考
ctrbf       可制御性ステアケース型の計算

obsv        可観測性行列の計算

参考文献

[1] Rosenbrock, M.M., State-Space and Multivariable Theory, John Wiley, 1970.

obsv

ord2