Control System Toolbox関数リファレンス

ctrbf

可制御性ステアケース型の計算

表示

[Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C)
[Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C,tol)

詳細
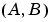の可制御性行列が、ランク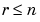の場合(ここで、n は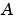のサイズ)、つぎのような相似変換が存在します。

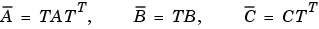
ここで、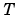はユニタリで、変換したシステムは左上部に不可制御モードが存在する場合、ステアケース型をもっています。

ここで、は可制御で、のすべての固有値は、不可制御かつ、

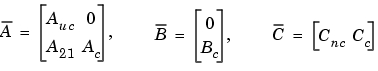
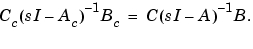
[Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C)となります。 [Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C)は、A、B、 Cで表わされる状態空間システムを、上に示すように可制御性ステアケース型Abar、Bbar、Cbarに分解します。Tは相似変換行列で、kは長さnのベクトルです。ここで、nはAが表すシステムの次数です。kの各成分は、変換行列計算の各段階で因数分解された可制御状態数を表します。kの中の非ゼロ要素の数は、Tを計算するのに必要とされた繰り返し回数を示しています。sum(k)は、Abarの可制御部分である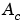中の状態数です。

ctrbf(A,B,C,tol)は、可制御/不可制御部分空間を計算するとき、トレランスtolを使用します。トレランスを設定しない場合、デフォルトとして、部分空間10*n*norm(A,1)*epsに設定されます。

例題

つぎの行列に対する可制御性ステアケースを計算します。

A =
     1     1
     4    -2

B =
     1    -1
     1    -1

C =
     1     0
     0     1

また、不可制御モードを探します。

[Abar,Bbar,Cbar,T,k]=ctrbf(A,B,C)

Abar =
   -3.0000         0
   -3.0000    2.0000

Bbar =
    0.0000    0.0000
    1.4142   -1.4142

Cbar =
   -0.7071    0.7071
    0.7071    0.7071

T =
   -0.7071    0.7071
    0.7071    0.7071
k =
     1     0

分解したシステムAbarは、-3の位置に不可制御モード、および、2の位置に可制御モードを示します。

また、システムの最小実現を見つけるために、ctrbfを用いる関数minrealも参照してください。

アルゴリズム

ctrbfは、[1]のステアケースアルゴリズムを実行するM-ファイルです。

参考
ctrb        可制御性行列の作成

minreal     最小実現と極零相殺

参考文献

[1] Rosenbrock, M.M., State-Space and Multivariable Theory, John Wiley, 1970.

ctrb

d2c