covar (Control System Toolbox関数リファレンス)

白色ノイズによって励起されるシステムの出力および状態共分散の計算

表示

[P,Q] = covar(sys,W)

詳細

covarは、ガウス白色ノイズ入力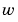によって励起される LTIモデルsysの出力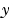の定常共分散を計算します。この関数は、連続系、離散系のいずれのケースも取り扱います。

P = covar(sys,W) は、定常状態出力応答共分散、

を、つぎのノイズ強度が与えられた場合に出力します。

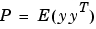
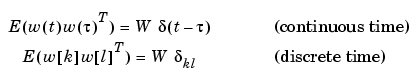
[P,Q] = covar(sys,W) は、sysが状態空間モデルのときに、定常状態の状態の共分散

も出力します(それ以外の場合、Qは []に設定)。

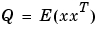
N-次元LTI配列sysに適用すると、covar は、つぎのような多次元配列P,Qを出力します。

すなわち、P(:,:,i1,...iN)とQ(:,:,i1,...iN)は、モデルsys(:,:,i1,...iN)に対する共分散行列です。

例題

つぎの離散SISOシステムに

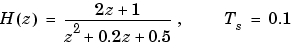
強度W = 5のGauss白色ノイズを適用したときの出力応答共分散を計算します。

sys = tf([2 1],[1 0.2 0.5],0.1);
p = covar(sys,5)

MATLABは、つぎの出力を行います。

p =
    30.3167

つぎのシミュレーション結果と比較します。

randn('seed',0)
w = sqrt(5)*randn(1,1000);  % 1000 サンプル

% LSIMでwに対する応答をシミュレーション
y = lsim(sys,w);

% 値 y の共分散を計算
psim = sum(y .* y)/length(w);

この結果は、つぎのようになります。

psim = 
    32.6269

2つの共分散値pとpsimは、有限シミュレーション区間(時間)で比較しているため完全には一致しません。

アルゴリズム

伝達関数および零点-極-ゲインモデルは、まず、ssで状態空間型に変換されます。

連続系状態空間モデルの場合、

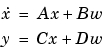
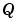は、つぎのLyapunov方程式を解くことによって求められます。

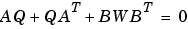
出力応答共分散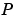は、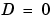の場合にのみ有限で、そのとき、つぎのようになります。

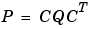
離散系では、状態共分散は、つぎの離散系Lyapunov方程式を解き、

は、次式で与えられます。

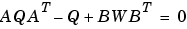
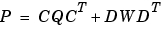
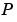は、離散系の場合、ゼロでない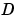に対して適切に定義されることに、注意してください。

制限

状態と出力の共分散は、安定したシステムに対してのみ定義されます。連続系の場合、出力応答共分散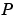は、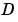行列がゼロ(厳密な意味でプロパなシステム)の場合にのみ有限です。

参考
dlyap 離散系Lyapunov方程式の解

lyap 連続系Lyapunov方程式の解

参考文献

[1] Bryson, A.E. and Y.C. Ho, Applied Optimal Control, Hemisphere Publishing, 1975, pp. 458-459.

connect ctrb