MATLAB Function Reference

residue

部分分数展開と多項式係数間の変換

表示

[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)

詳細

関数 residue は、多項式の商から極-留数表現への変換および逆変換を行います。

[r,p,k] = residue(b,a) は、つぎの型の 2 つの多項式 b(s) と a(s) の比を部分分数展開して、留数、極、直接項を求めます。

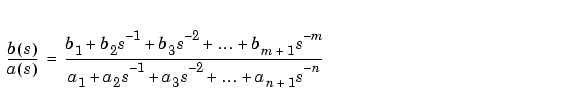
[b,a] = residue(r,p,k) は、部分分数展開を、係数 b と a による多項式に変換します。

定義

重根がない場合は、つぎのようになります。

極の個数 n は、つぎのようになります。

n = length(a)-1 = length(r) = length(p)

直接項の係数ベクトルは、length(b) < length(a) の場合、空ベクトルで、その他の場合、つぎのようになります。

length(k) = length(b)-length(a)+1

p(j) = ... = p(j+m-1) が多重度 m の極の場合、展開はつぎの型の項を含むことになります。

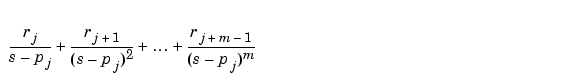
引数

b,a	s の降べき順で多項式の係数を指定するベクトル
r	留数の列ベクトル
p	極の列ベクトル
k	直接項の行ベクトル

アルゴリズム

residue は、M-ファイルです。まず、roots で極を求めます。つぎに、分数がプロパでない場合は、直接項 k は deconv を使って多項式の長除法で求めます。最後に、留数は削除される個々の根で多項式を計算して求めます。根に対して、M-ファイル resi2 は重根の位置での留数を計算します。

制限

数値的に、多項式の比の部分分数展開は適切な問題ではありません。分母多項式 a(s) が重根をもつ多項式に近い場合、丸め誤差を含むデータの小さな変化が、極や留数の結果を大きく変化させます。状態空間または零点-極表現を使った問題の定式化の方が好ましいといえます。

参考

deconv, poly, roots

参考文献

[1] Oppenheim, A.V. and R.W. Schafer, Digital Signal Processing, Prentice-Hall, 1975, p. 56.

reshape

return