MATLAB Function Reference

quad, quad8

数値積分、最適 Simpson 求積法

注意    関数 quad8 は、古い関数です。関数 quadl に置き換えることをお勧めします。

表示

q = quad(fun,a,b)
q = quad(fun,a,b,tol)
q = quad(fun,a,b,tol,trace)
q = quad(fun,a,b,tol,trace,p1,p2,...)

詳細

q = quad(fun,a,b) は、a から b までの区間で、再帰的な適応 Simpson 求積法を使って、丸め誤差の範囲内で、関数 fun の積分を近似します。fun は、ベクトル x を受け取り、ベクトル y を戻します。関数 fun は、x の各要素について、計算されます。

求積 は、関数のグラフの下の部分を求めるために使用する数値法で、定積分を計算します。

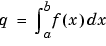
q = quad(fun,a,b,tol) は、デフォルトの 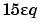の代わりに、絶対誤差許容範囲 tol を使います。ここで、 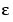は、浮動小数点精度 eps で、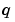 は、積分により求められたものです。tol を大きい値にすると、関数計算の回数が減り、計算は速くなります。しかし、結果の精度は低くなります。MATLAB version 5.3 やそれ以前のバージョンで、関数 quad は、精度の低いアルゴリズムを使っていて、デフォルトの相対許容誤差は、1.0e-3 です。

q = quad(fun,a,b,tol,trace) 引数 trace がゼロでない場合は、リカーシブな作業を行っている間、[fcnt a b-a Q] の値を示します。

q = quad(fun,a,b,tol,trace,p1,p2,...) は、付加的な引数 p1,p2,... を、関数 fun, fun(x,p1,p2,...) に直接、渡すことができます。tol、または、trace に対して空行列を渡すと、デフォルト値が使われます。

例題

例題 1. fun の設定に3つの異なる方法を使うことができます。

• 単変数を含んだ文字列表現

Q = quad('1./(x.^3-2*x-5)',0,2); 

• インラインオブジェクト

F = inline('1./(x.^3-2*x-5)'); 
Q = quad(F,0,2); 

• 関数ハンドル

Q = quad(@myfun,0,2); 

ここで、myfun.m は、M-ファイルです。

function y = myfun(x) 
y = 1./(x.^3-2*x-5);

例題 2. 正弦関数を 0 から まで、積分します。

a = quad(@sin,0,pi)

a =

    2.0000

参考

dblquad, inline, quadl, @ (関数ハンドル)

参考文献

Forsythe, G.E., M.A. Malcolm and C.B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1977.

Gander, W. and W. Gautschi, "Adaptive Quadrature - Revisited", BIT, Vol. 40, 2000, pp. 84-101. このドキュメントは、http://www.inf.ethz.ch/personal/gander　を通して、利用できます。

qrupdate

quadl