qrupdate (MATLAB Function 参考文献)

オリジナル行列にランク1の行列を加えたもののQR分解

表示

[Q1,R1] = qrupdate(Q,R,u,v)

詳細

[Q1,R1] = qrupdate(Q,R,u,v) は、[Q,R] = qr(A) がオリジナルのA のQR分解のとき、A + u*v'のQR分解を出力します。このとき、uとvは、適切な長さの列ベクトルです。

注意

qrupdate は、フル行列に対してのみ機能します。

例題

行列

mu = sqrt(eps)

mu =

   1.4901e-08

A = [ones(1,4); mu*eye(4)];

は、A'*Aの作成での危険性を示す最小二乗で良く知られた例です。代わりに、直交行列Qと上三角行列RへのQR分解を使います。

 [Q,R] = qr(A);

予想した通り、Rは上三角行列になります。

R =

   -1.0000   -1.0000   -1.0000   -1.0000
         0    0.0000    0.0000    0.0000
         0         0    0.0000    0.0000
         0         0         0    0.0000
         0         0         0         0

この場合、最初の行を除くRの上三角要素はsqrt(eps)の大きさです。

アップデートベクトルを、つぎのように考えます。

 u = [-1 0 0 0 0]'; v = ones(4,1);

つぎのように、Aにランク1の行列を加えたQR分解を計算する代わりに、

[QT,RT] = qr(A + u*v')

QT =

     0     0     0     0     1
    -1     0     0     0     0
     0    -1     0     0     0
     0     0    -1     0     0
     0     0     0    -1     0

RT =

   1.0e-07 *
   -0.1490         0         0         0
         0   -0.1490         0         0
         0         0   -0.1490         0
         0         0         0   -0.1490
         0         0         0         0

qrupdate を使うことができます。

[Q1,R1] = qrupdate(Q,R,u,v)

Q1 =

   -0.0000   -0.0000   -0.0000   -0.0000    1.0000
    1.0000   -0.0000   -0.0000   -0.0000    0.0000
   -0.0000    1.0000   -0.0000   -0.0000    0.0000
   -0.0000   -0.0000    1.0000   -0.0000    0.0000
         0         0         0    1.0000    0.0000

R1 =

   1.0e-07 *
    0.1490    0.0000    0.0000    0.0000
         0    0.1490   -0.0000   -0.0000
         0         0    0.1490   -0.0000
         0         0         0    0.1490
         0         0         0         0

両方の分解は異なっていても、正しいことに注意してください。

アルゴリズム

qrupdate は、Golub and van Loanの、Matrix Computationsの第3版の12.5.1節のアルゴリズムを使用します。N = max(m,n) の場合、何もない場合から新規のQR分解を計算するのは、ほぼ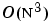、のアルゴリズムで、この方法で既存の因子にランク1の行列を加えるのは、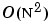アルゴリズムであるため、qrupdate は有効です。

参考文献

Golub, Gene H. and Charles Van Loan, Matrix Computations, Third Edition, Johns Hopkins University Press, Baltimore, 1996

参考

cholupdate, qr

qrinsert quad, quad8