| MATLAB Function Reference | |
表示
p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)
詳細
p = polyfit(x,y,n)
は、最小二乗の意味で、データ p(x(i)) を y(i) にフィットするため、次数 n の多項式 p(x) の係数を求めます。結果の p は、多項式の係数を要素とする長さ n+1 の行ベクトルで、次数の高い順に並べています。
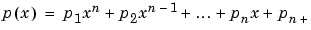
[p,S] = polyfit(x,y,n)
は、誤差推定、または、予測誤差を得るため、polyval を使って、多項式の係数p と構造体 S を戻します。データ y の中に含まれる誤差が、一定の分散をもち、独立で、正規分布をしている場合、polyval は、予測の少なくとも 50% を含む誤差境界を作成します。
[p,S,mu] = polyfit(x,y,n)
は、つぎの多項式の係数を求めます。
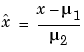
ここで、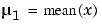
と 
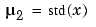です。mu は、2要素ベクトル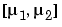 
です。この中心に関する変換とスケーリングに関する変換は、多項式アルゴリズムとフィッテングアルゴリズム共に、数値的な性質を改良します。
例題
つぎの例では、x の多項式で誤差関数 erf(x) を近似します。erf(x) は有界な関数ですが、多項式は有界でないので、近似はうまくいきません。
区間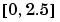 
に等間隔に分布する x 点をもつベクトルを作ることから始めます。そして、これらの点で、erf(x) を計算します。
x = (0: 0.1: 2.5)'; y = erf(x);
p = polyfit(x,y,6)
p =
0.0084 -0.0983 0.4217 -0.7435 0.1471 1.1064 0.0004
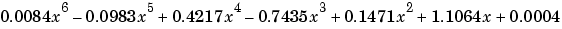
どの程度良く近似されているかを見るには、データ点で多項式を計算します。
f = polyval(p,x);
table = [x y f y-f]
table =
0 0 0.0004 -0.0004
0.1000 0.1125 0.1119 0.0006
0.2000 0.2227 0.2223 0.0004
0.3000 0.3286 0.3287 -0.0001
0.4000 0.4284 0.4288 -0.0004
...
2.1000 0.9970 0.9969 0.0001
2.2000 0.9981 0.9982 -0.0001
2.3000 0.9989 0.9991 -0.0003
2.4000 0.9993 0.9995 -0.0002
2.5000 0.9996 0.9994 0.0002
この区間では、近似は 3桁から 4桁の間までは良く一致します。しかし、この区間を超えると、多項式の値に対する近似が急激に悪くなることがグラフからわかります。
x = (0: 0.1: 5)'; y = erf(x); f = polyval(p,x); plot(x,y,'o',x,f,'-') axis([0 5 0 2])
アルゴリズム
polyfit M-ファイルは、Vandermonde 行列 V を作成します。この行列要素は、x のベキ乗の型をしています。
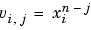
そして、バックシュラッシュ演算子 \ を使って、最小二乗問題を解きます。
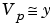
M-ファイルを修正して、x の他の関数を基本関数として使うことができます。
参考
| | polyeig | polyval | |
