

| MATLAB Function Reference |   |
表示
[X,e] = polyeig(A0,A1,...Ap)
詳細
[X,e] = polyeig(A0,A1,...Ap)
は、p次の多項式固有値問題を解きます。
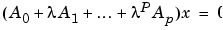
ここで、多項式の次数 p は負でない整数で、A0,A1,...Ap は、n次の入力行列です。出力行列 X は、n行n*p列で、各列は固有ベクトルです。出力ベクトル e は、長さ n*p で、固有値を含みます。
注意
p と n の値に基づいて、polyeig はいくつかの特殊な場合を扱います。
p = 0 、または、polyeig(A) は、標準の固有値問題で、eig(A) と同じです。p = 1 、または、polyeig(A,B) は、一般化固有値問題で、eig(A,-B) と同じです。n = 1、または、スカラ a0, a1 ..., ap に対する polyeig(a0,a1,...ap) は、標準の多項式問題で、roots([ap ... a1 a0]) と同じです。アルゴリズム
A0と Ap の両方が正則でない場合、問題は潜在的に悪い状態です。すなわち、解は存在しないか、または一意的ではありません。この場合、求められた解は正確ではないかもしれません。polyeigは、この状況を検出し、適切なワーニングメッセージを表示します。A0 と Ap のうちのいずれか1つでも正則ならば、問題は良い状態ですが、固有値のいくつかはゼロまたは無限大(Inf) となるかもしれません。
polyeig は、一般化固有値の計算で中間結果を求めるために、QZ分解を使います。固有値がうまく決定される場合、中間結果を使います。これに関する詳細は、eig, qz の記述を参照してください。
参考
 | polyder | polyfit |  |