Getting Started

多次元配列

MATLABの多次元配列は、2つ以上のサブスクリプトをもった配列です。これは、3つ以上の引数と共に zeros, ones, rand, randn を使って作成されます。たとえば、

R = randn(3,4,5);

は、3x4x5 = 60個の正規分布する乱数要素をもつ3x4x5の配列を作成します。

3次元配列は、3次元の物理的データを表わします。たとえば、長方形グリッド上でサンプリングした室温を表わします。また、行列の数列A^(k) や時間依存行列のサンプルA(t) を表わします。後者の場合、k 番目の行列、またはt_k 番目の行列の(i, j) 番目の要素は、A(i,j,k) によって表わされます。

4次の魔方陣のMATLABバージョンとDürerバージョンは、2つの列が入れ替わっています。列を入れ替えることにより、異なる魔方陣を作ることができます。ステートメント

p = perms(1:4);

は、1:4の順列4! = 24の組合せがあります。k 番目の順列は、行ベクトル p(k,:) です。それで、

A = magic(4);
M = zeros(4,4,24);
for k = 1:24
   M(:,:,k) = A(:,p(k,:));
end

は、3次元配列 M に24種の魔方陣を格納します。M の大きさは、

size(M)

ans =
     4     4    24

22番目の行列がDürerの魔方陣であることがわかります。

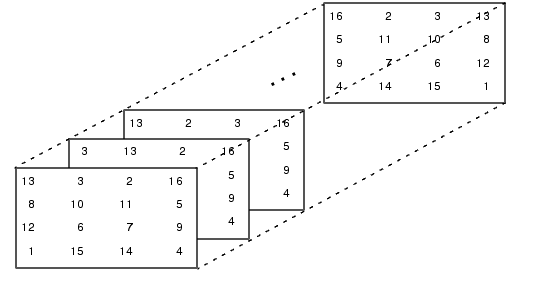
M(:,:,22)

ans =
    16     3     2    13
     5    10    11     8
     9     6     7    12
     4    15    14     1

ステートメント

sum(M,d)

は、d 番目のサブスクリプトを変更して和を計算します。

sum(M,1)

は、24個の行ベクトル

34    34    34    34

を含む1x4x24配列になります。そして、

sum(M,2)

は、24個の列ベクトル

34    
34    
34    
34

を含む4x1x24配列になります。最終的に、

S = sum(M,3)

は、24個の行列を足したものなります。結果は4x4x1になり、4行4列の配列に見えます。

S =
   204   204   204   204
   204   204   204   204
   204   204   204   204
   204   204   204   204

その他のデータ構造

セル配列