Spline Toolbox

The B-form

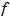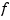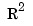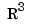A univariate spline is specified by its nondecreasing knot sequence t and by its B-spline coefficient sequence a -- see Tensor Product Splines for a discussion of multivariate splines. The coefficients may be d-vectors, usually 2-vectors or 3-vectors and required to be written as 1-column matrices, in which case is a curve in or and the coefficients are called the control points for the curve.

Roughly speaking, such a spline is piecewise-polynomial of a certain order and with breaks 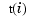. But knots are different from breaks in that they may be repeated, i.e., t need not be strictly increasing. The resulting knot multiplicities govern the smoothness of the spline across the knots, as detailed below.

With [d,n] = size(a), and n+k = length(t), the spline is of order k. This means that its polynomial pieces have degree < k. For example, a cubic spline is a spline of order 4 since it takes four coefficients to specify a cubic polynomial.

This section treats these aspects of the B-form:

• B-form
• B-Splines
• Knot Multiplicity
• Choice of Knots
• Splines
• Construction
• Example: A Spline Curve
• Use

Use

B-form