| Spline Toolbox | |
Use
The following commands are available for spline work. There is spmak and fnbrk to make up a spline and take it apart again. Use fn2fm to convert from B-form to ppform. You can evaluate, differentiate, integrate, plot, or refine a spline with the aid of fnval, fnder, fndir, fnint, fnplt, and fnrfn.
There are five commands for generating knot sequences:
augknt for providing boundary knots and also controlling the multiplicity of interior knots
brk2knt for supplying a knot sequence with specified multiplicities
aptknt for providing a knot sequence for a spline space of given order that is suitable for interpolation at given data sites
optknt for providing an optimal knot sequence for interpolation at given sites
newknt for a knot sequence perhaps more suitable for the function to be approximated
aveknt to supply certain knot averages (the Greville sites) as recommended sites for interpolation
chbpnt to supply such sites
knt2brk and knt2mlt for extracting the breaks and/or their multiplicities from a given knot sequence
To display a spline curve with given two-dimensional coefficient sequence and a uniform knot sequence, use spcrv.
You can also write your own spline construction commands, in which case you will need to know the following. The construction of a spline satisfying some interpolation or approximation conditions usually requires a collocation matrix, i.e., the matrix that, in each row, contains the sequence of numbers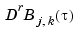 
, i.e., the 
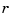th derivative at 
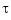of the 
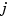th B-spline, for all 
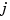, for some 
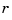and some site 
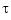. Such a matrix is provided by spcol. An optional argument allows for this matrix to be supplied by spcol in a space-saving spline-almost-block-diagonal-form or as a MATLAB sparse matrix. It can be fed to slvblk, a command for solving linear systems with an almost-block-diagonal coefficient matrix. If you are interested in seeing how spcol and slvblk are used in this toolbox, have a look at the commands spapi, spap2, and spaps.
In addition, there are routines for constructing cubic splines. csapi and csape provide the cubic spline interpolant at knots to given data, using the not-a-knot and various other end conditions, respectively. A parametric cubic spline curve through given points is provided by cscvn. The cubic smoothing spline is constructed in csaps.
The remaining commands involving the B-form are utilities, of no interest to the casual user.
| | Example: A Spline Curve | Tensor Product Splines | |