Spline Toolbox

Example: A Spline Curve

As another simple example,

• points = .95*[0 -1 0 1;1 0 -1 0]; 
  sp = spmak(-4:8,[points points]);
  

provides a planar, quartic, spline curve whose middle part is a pretty good approximation to a circle, as the plot on the next page shows. It is generated by a subsequent

• plot(points(1,:),points(2,:),'x'), hold on 
  fnplt(sp,[0,4]), axis equal square, hold off
  

Insertion of additional control points 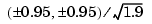would make a visually perfect circle.

Here are more details. The spline curve generated has the form 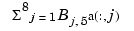, with -4:8 the uniform knot sequence, and with its control points 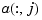the sequence

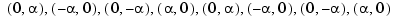with 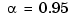. Only the curve part between the parameter values 0 and 4 is actually plotted.

To get a feeling for how close to circular this part of the curve actually is, we compute its unsigned curvature. The curvature 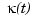at the curve point 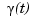of a space curve 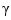can be computed from the formula

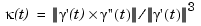
in which 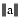is the Euclidean length of the 3-vector a, and 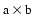is the cross product of the two 3-vectors a and b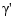, and and 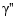are the first and second derivative of the curve with respect to the parameter used. We treat our planar curve as a space curve in the 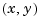-plane, hence obtain the maximum and minimum of its curvature at 21 points as follows:

• t = linspace(0,4,21);zt = zeros(size(t));
  dsp = fnder(sp); dspt = fnval(dsp,t); ddspt = 
  fnval(fnder(dsp),t);
  kappa = abs(dspt(1,:).*ddspt(2,:)-dspt(2,:).*ddspt(1,:))./...
     (sum(dspt.^2)).^(3/2);
  [min(kappa),max(kappa)] 
  >> ans = 1.6747    1.8611
  

So, while the curvature is not quite constant, it is close to 1/radius of the circle, as we see from the next calculation:

• 1/norm(fnval(sp,0)) 
  ans = 1.7864 
  
  
  

Figure 2-12: Spline Approximation to a Circle; Control Points Are Marked x

Construction

Use