Spline Toolbox

Choice of Knots

The rule "knot multiplicity + condition multiplicity = order" has the following consequence for the process of choosing a knot sequence for the B-form of a spline approximant. Suppose the spline 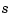is to be of order 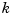, with basic interval 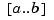, and with interior breaks 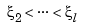. Suppose, further, that, at 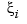, the spline is to satisfy 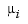smoothness conditions, i.e.,  

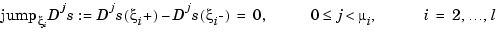
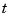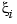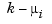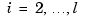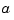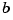Then, the appropriate knot sequence should contain the break exactly times, . In addition, it should contain the two endpoints, and , of the basic interval exactly 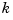times. This last requirement can be relaxed, but has become standard. With this choice, there is exactly one way to write each spline s with the properties described as a weighted sum of the B-splines of order 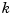with knots a segment of the knot sequence 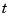. This is the reason for the B in B-spline: B-splines are, in Schoenberg's terminology, basic splines.

For example, if you want to generate the B-form of a cubic spline on the interval [1 . . 3], with interior breaks 1.5, 1.8, 2.6, and with two continuous derivatives, then the following would be the appropriate knot sequence:

• t = [1, 1, 1, 1, 1.5, 1.8, 2.6, 3, 3, 3, 3];
  

This is supplied by augknt([1, 1.5, 1.8, 2.6, 3], 4). If you wanted, instead, to allow for a corner at 1.8, i.e., a possible jump in the first derivative there, you would triple the knot 1.8, i.e., use

• t = [1, 1, 1, 1, 1.5, 1.8, 1.8, 1.8, 2.6, 3, 3, 3, 3];
  

and this is provided by the statement

• t = augknt([1, 1.5, 1.8, 2.6, 3], 4, [1, 3, 1] );
  

Knot Multiplicity

Splines