| Spline Toolbox | |
Directional derivative of a function
Syntax
Description
df = fndir(f,y)
is the ppform of the directional derivative, of the function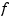 
in f, in the direction of the (column-)vector y. This means that df describes the function
.
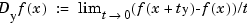If y is a matrix, with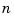 
columns, and 
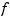is 
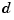-valued, then the function in df is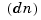 
-valued. Its value at 
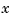, reshaped as a matrix of size 
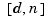, has in its 
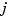th column the directional derivative of 
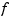at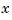 
in the direction of the 
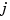th column of y.
Since fndir relies on the ppform of the function in f, it does not work for rational functions nor for functions in stform.
Examples
For example, if f describes an m-variate d-vector-valued function and x is some point in its domain, then, e.g., with this particular ppform f that describes a scalar-valued bilinear polynomial,
f = ppmak({0:1,0:1},[1 0;0 1]); x = [0;0]; d = fnbrk(f,'dim'); m = fnbrk(f,'var'); jacobian = reshape(fnval(fndir(f,eye(m)),x),d,m)
is the Jacobian of that function at that point (which, for this particular scalar-valued function, is its gradient, and it is zero at the origin).
As a related example, the next statements plot the gradients of (a good approximation to) the Franke function at a regular mesh:
xx = linspace(-.1,1.1,13); yy = linspace(0,1,11); [x,y] = ndgrid(xx,yy); z = franke(x,y); pp2dir = fndir(csapi({xx,yy},z),eye(2)); grads = reshape(fnval(pp2dir,[x(:) y(:)].'),... [2,length(xx),length(yy)]); quiver(x,y,squeeze(grads(1,:,:)),squeeze(grads(2,:,:)))
Algorithm
The function in f is converted to ppform, and the directional derivative of its polynomial pieces is computed formally and in one vector operation, and put together again to form the ppform of the directional derivative of the function in f.
See Also
| | fnder | fnint | |
