Robust Control Toolbox

Parametrization of all realizable stable closed-loop systems for use in infinity-norm controller synthesis.

Syntax

• youla 
    Inputs: A, B1, B2, C1, C2, D11, D12, D21, D22 
    Outputs: at11, bt11, ct11, dt11 
       at12, bt12, ct12, dt12, at1p, bt1p, ct1p, dt1p 
       at21, bt21, ct21, dt21, at2p, bt2p, ct2p, dt2p 
       kx, x, ky, y, f, h
  

Description
youla is a script M-file used as a subroutine by the script M-file linf. Given an "augmented plant" P(s) having state-space matrices

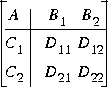
youla computes an LQG controller K(s) such that the closed-loop system T(s) shown in Figure 1-18 has the form

with T₁₂ and T₂₁ inner, i.e.

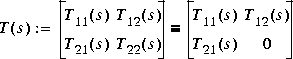
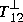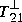Youla also computes complementary inner-factors and such

that 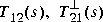and 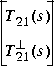are square and inner. A realization for

is returned as

Figure 1-18: Youla Parametrization.

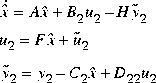
The state-feedback Riccati solution and the Kalman-Bucy filter Riccati equation are returned as x and y respectively. Also returned are the associated gain matrices f and h.

As shown by [3], the closed-loop transfer function of the system in Figure 1-19 is the Youla parameterization of the set of realizable stable closed-loop transfer functions, viz.,

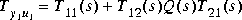
where Q(s) is any stable transfer function matrix.

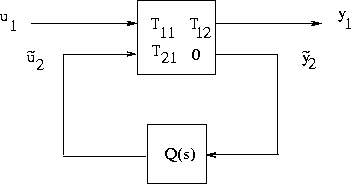
Figure 1-19: Q-Parametrization.

Algorithm
We employ the formulae of [2], as reported in the paper [4]:

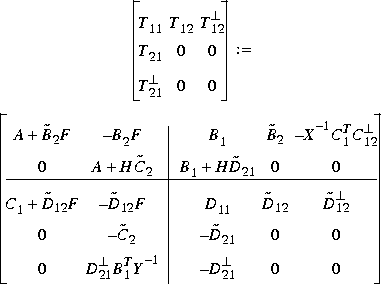
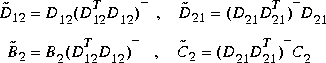
where X^-1 and Y^-1 are pseudo inverses, and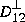

and and 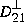are computed using ortc and ortr such that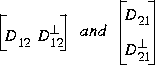

are both unitary. The variables f, x, h, y are computed as the solution of LQ optimal control problems via the MATLAB commands:

• [kx,x] = lqrc(A,B2,C1'*C1,D12'*D12,C1'*D12);
  [ky,y] = lqrc(A',C2',B1*B1',D21*D21',B1*D21'); 
  f = -kx; 
  h = -ky';
  

See Also
h2lqg, hinf, hinfdemo, linf, linfdemo

References
[1] C. A. Desoer, R. W. Liu, J. Murray and R. Saeks, "Feedback System Design: The Fractional Representation Approach to Analysis and Synthesis," IEEE Trans. on Automat. Control, June, 1980.

[2] J. Doyle, Advances in Multivariable Control. Lecture Notes at ONR/Honeywell Workshop. Minneapolis, MN, Oct. 8-10, 1984.

[3] C. N. Nett, C. A. Jacobson, and M. J. Balas, "A Connection Between State-Space and Doubly Coprime Fractional Representations," IEEE Trans. on Automat. Control, AC-29, Sep. 1984.

[4] M. G. Safonov, E. A. Jonckheere, M. Verma and D. J. N. Limebeer, "Synthesis of Positive Real Multivariable Feedback Systems", Int. J. Control, vol. 45, no. 3, pp. 817-842, 1987.

tree, istree