ohkapp, ohklmr (Robust Control Toolbox)

Robust Control Toolbox

ohkapp, ohklmr

Optimal Hankel minimum degree approximation without balancing.

Syntax

[ax,bx,cx,dx,ay,by,cy,dy,aug] = ohkapp(a,b,c,d,Type)
[ax,bx,cx,dx,ay,by,cy,dy,aug] = ohkapp(a,b,c,d,Type,in)
[am,bm,cm,dm,totbnd,svh] = ohklmr(a,b,c,d,Type) 
[am,bm,cm,dm,totbnd,svh] = ohklmr(a,b,c,d,Type,in)
[ssx,ssy,] = ohkapp(ss,) 
[ssm,] = ohklmr(ss,..)

Description
ohkapp computes the kth order optimal Hankel minimum degree approximation (OHMDA)

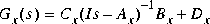
of a possibly non-minimal nth order stable system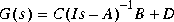

such that G_x is stable and

where 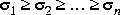denote Hankel singular values of G(s), i.e., the square roots of eigenvalues of PQ, where P and Q are the reachability and observability grammians of (A, B, C, D).

An anticausal G_y(s) is also returned in (A_y, B_y, C_y, D_y). Together G_x(s) and G_y(s) possess the following important property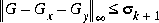

[ax,bx,cx,dx,ay,by,cy,dy,aug] = ohkapp(a,b,c,d,1,0) computes the zeroth order OHMDA, i.e., the anticausal OHMDA of a stable system, which is an important intermediate step of the L control synthesis.

Variable aug contains the following information:

aug(1,1) = ₁aug(1,2) = number of states removed 
aug(1,3) = totbnd 
aug(4:4+n-1) = [₁, _2,..., _n].

ohklmr also computes the k_th order OHMDA, but allows the system to be unstable. It works by applying ohkapp to the stable and antistable parts of G(s) (obtained via stabproj), then applying addss. Totbnd returns the L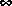

norm error bound of the approximation. Variable svh returns the Hankel singular values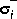

of [G(s)]- (stable part) and

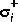of [G(-s)]+ (reversed antistable part), i.e.,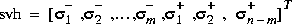

where m denotes the number of stable roots, n- m denotes the number of unstable roots.

Both ohkapp and ohklmr provide three options:

1: Type = 1, in = k, size of reduced order model.

2: Type = 2, in = tol, find a kth order reduced model such that the total error totbnd is less than tol.

3: Type = 3, display svh and prompt for k + 1. In this case, there is no need to assign a value for in.

Algorithm
ohkapp and ohklmr employ the algorithm described in [3], which is a "basis-free" descriptor system implementation of the OHMDA. The descriptor formulae bypass the numerically ill-conditioned balanced realization step required by the earlier state-space formulae [1, 2].

ohklmr uses the M-function stabproj to split G(s) into the sum of stable and antistable parts, then applies ohkapp to each part.

References
[1] M. Bettayeb, L. M. Silverman and M. G. Safonov, "Optimal Approximation of Continuous Time Systems," IEEE Conf. on Decision and Control, Albuquerque, NM, Dec. 10-12, 1981.

[2] K. Glover, "All Optimal Hankel Norm Approximation of Linear Multivariable Systems, and Their L-error Bounds," Int. J. Control, vol. 39, no. 6, pp. 1145-1193, 1984.

[3] M. G. Safonov, R. Y. Chiang, and D. J. N. Limebeer, "Hankel Model Reduction without Balancing -- A Descriptor Approach," Proc. IEEE Conf. on Decision and Control, Los Angeles, CA, Dec. 9-11, 1987, also "Optimal Hankel Model Reduction for Nonminimal Systems," IEEE Trans. on Automat. Contr., vol. 34, no. 4, pp. 496-502, 1990.

obalreal osborne