obalreal (Robust Control Toolbox)

Robust Control Toolbox

obalreal

Balanced realization via B. C. Moore's algorithm.

Syntax

```
[abal,bbal,cbal,g,t] = obalreal(a,b,c)
```

Description
This M-file does functionally the same thing as balreal, but the balanced reachability and observability grammians (P and Q) are ordered and
P = Q = diag(g). The similarity transformations are accumulated in the variable t. Moore's [1] kth-order reduced model G_k(s) can be simply extracted from the balanced state-space

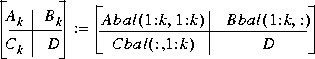
obalreal is an M-file that implements the algorithm of [1]. Balreal uses the Cholesky decomposition to find the associated left and right eigenspaces of PQ. Obalreal is superior to the existing balreal M-file in two ways:

1: Grammians are ordered.

2: Transformations are carried out using reliable SVD's.

What makes balanced realization important is not only its structure but also L

the norm error bound associated with its kth order reduced model ([2] and [3]):

Therefore, you can anticipate how big an error the reduced model will have before actually doing the model reduction.

Limitations
The original system (A, B, C, D) has to be minimal, otherwise the balancing algorithm in either obalreal [1] or balreal [4] breaks down. See schmr and balmr for robust methods for computing G_k without balancing.

See Also
balreal, balmr, schmr, schbal, ohklmr, ohkapp, reschmr

References
[1] B. C. Moore, "Principal Component Analysis in Linear Systems: Controllability, Observability and Model Reduction," IEEE Trans. on Automat. Contr., AC-26, pp. 17-31, February 1981.

[2] D. F. Enns, "Model Reduction with Balanced Realizations: An Error Bound and Frequency-Weighted Generalization," Proc. IEEE Conf. on Decision and Control, Las Vegas, NV, Dec. 12-14, 1984.

[3] K. Glover, "All Optimal Hankel Norm Approximations of Linear Multivariable Systems, and Their L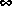-error Bounds," Int. J. Control, vol. 39, no. 6, pp. 1145-1193, 1984.

[4] A. J. Laub, M. T. Heath, C. C. Page, and R. C. Ward, "Computation of balancing transformations and other applications of simultaneous diagonalization algorithms," IEEE Trans. on Automat. Contr., AC-32, pp. 115-122, 1987.

[5] M. G. Safonov and R. Y. Chiang, "A Schur Method for Balanced Model Reduction," IEEE Trans. on Automat. Contr., vol. AC-34, no. 7, pp. 729-733, July 1989.

normhinf, normh2 ohkapp, ohklmr