Robust Control Toolbox

Compute the H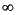 norm and H² norm of a system.

Syntax

• [h2n] = normh2(a,b,c,d) 
  [hinfn] = normhinf(a,b,c,d,aux) 
  [hinfn] = normhinf(a,b,c,d) 
  [h2n] = normh2(ss) 
  [hinfn] = normhinf(ss,aux) 
  [hinfn] = normhinf(ss)
  

Description
Given a stable system 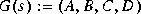, normh2 computes its H² norm and normhinf computes its H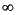 norm.

The computation of 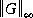requires a search, therefore an optional input variable of aux overrides default values for initializing the search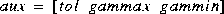

where tol terminates the search process (default=0.001), and gammax and gammin are initial guesses for upper and lower bounds on 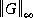. Defaults for gammax and gammin are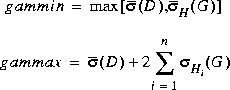

where the 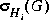's are the Hankel singular values of G(s). The bounds may be found among the results in [1, 2].

Algorithm
Consider a strictly proper, stable 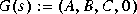. The two norm of G(s) is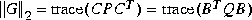

where P is the controllability grammian of (A, B) and Q is the observability grammian of (C, A) computed by gram.

For computing the H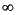 norm, consider the following fact:

Given a 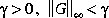, if and only if the right spectral factorization (cf. sfr.m) Hamiltonian matrix

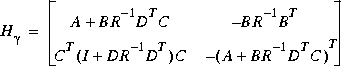
has no imaginary eigenvalues; here R = 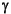²I - D^TD > 0.

normhinf uses a standard binary search to find the optimal 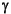similar to the algorithm used in hinfopt.

See Also
gram, hinf, hinfopt

References
[1] K. Glover, "All Optimal Hankel Norm Approximations of Linear Multivariable Systems, and Their L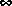-Error Bounds," Int. J. Control, vol. 39, no. 6, pp. 1145-1193, 1984.

[2] S. Boyd, V. Balakrishnan, and P. Kabamba, "In Computing the H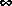 Norm of a Transfer Matrix," Mathematics of Control, Signals, and Systems, 1988.

musyn

obalreal