smpccon (Model Predictive Control Toolbox)

Model Predictive Control Toolbox

smpccon

Calculates MPC controller gain using a model in MPC mod format.

Syntax

Ks = smpccon(imod) 
Ks = smpccon(imod,ywt,uwt,M,P)

Description
Combines the following variables (most of which are optional and have default values) to calculate the state-space MPC gain matrix, Ks.

imod is the model of the process to be used in the controller design (in the mod format).

The following input variables are optional:

ywt
Is a matrix of weights that will be applied to the setpoint tracking errors. If you use ywt=[ ] or omit it, the default is equal (unity) weighting of all outputs over the entire prediction horizon. If ywt[ ], it must have ny columns, where ny is the number of outputs. All weights must be 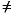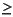0.

You may vary the weights at each step in the prediction horizon by including up to P rows in ywt. Then the first row of ny values applies to the tracking errors in the first step in the prediction horizon, the next row applies to the next step, etc.

If you supply only nrow rows, where 1 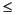nrow < P, smpccon will use the last row to fill in any remaining steps. Thus if you wish the weighting to be the same for all P steps, you need only specify a single row.

uwt
Same format as ywt, except that uwt applies to the changes in the manipulated variables. If you use uwt=[ ] or omit it, the default is zero weighting. If uwt[ ], it must have nu columns, where nu is the number of manipulated variables.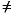

M
There are two ways to specify this variable:

If it is a scalar, smpccon interprets it as the input horizon (number of moves) as in DMC.

If it is a row vector containing nb elements, each element of the vector indicates the number of steps over which 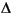u = 0 during the optimization and smpccon interprets it as a set of nb blocking factors. There may be 1 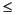nb 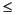P blocking factors, and their sum must be 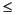P.

If you set M=[ ] or omit it, the default is M=P, which is equivalent to M=ones(1,P).

P
The number of sampling periods in the prediction horizon. If you set P=[ ] or omit it, the default is P=1.

If you take the default values for all the optional variables, you get the "perfect controller," i.e., a model-inverse controller. This controller is not applicable in the following situations:

When one or more outputs cannot respond to the manipulated variables within 1 sampling period due to time delay, the plant-inverse controller is unrealizable. To counteract this you can penalize changes in the manipulated variables (variable uwt), use blocking (variable M), and/or make P>>M.
When imod contains transmission zeros outside the unit circle the plant-inverse controller will be unstable. To counteract this, you can use blocking (variable M), restrict the input horizon (variable M), and/or penalize changes in the manipulated variables (variable uwt).

The model-inverse controller is also relatively sensitive to model error and is best used as a point of reference from which you can progress to a more robust design.

Algorithm
The controller gain is a component of the solution to the optimization problem:

Minimize

with respect to 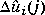(a series of current and future moves in the manipulated variables), where 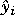(k + j) is a prediction of output i at a time j sampling periods into the future (relative to the current time, k), which is a function of 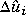(j), ri(k + j) is the corresponding future setpoint, and nb is the number of blocks or moves of the manipulated variables.

References
Ricker, N. L. "Use of Quadratic Programming for Constrained Internal Model Control," Ind. Eng. Chem. Process Des. Dev., 1985, 24, 925-936.

Ricker, N. L. "Model-predictive control with state estimation," I & EC Res., 1990, 29, 374.

Example
Consider the linear system:

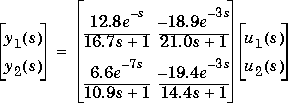
See the smpccl example for the commands that build the model and a simple controller for this process.

Here is a slightly more complex design with blocking and time-varying weights on the manipulated and output variables:

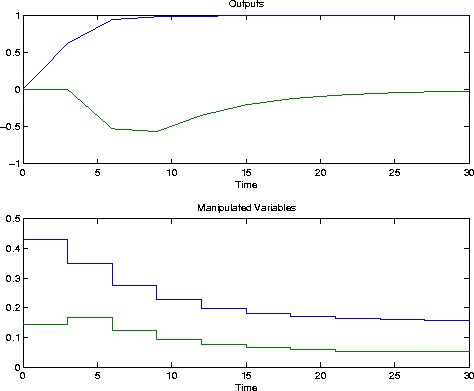
P=6; M=[2 4]; 
 uwt=[1 0; 0 1];
 ywt=[1 0.1; 0.8 0.1; 0.1 0.1];
 Ks=smpccon(imod,ywt,uwt,M,P);
 tend=30; r=[1 0];
 [y,u]=smpcsim(pmod,imod,Ks,tend,r);

There is no particular rationale for using time varying weights in this case -- it is only for illustration. The manipulated variables will make 2 moves during the prediction horizon (see value of M, above). The uwt selection gives u1 a unity weight and u2 a zero weight for the first move, then switches the weights for the second move. If there had been any additional moves they would have had the same weighting as the second move.

The ywt value assigns a constant weight of 0.1 to y₂, and a weight that decreases over the first 3 periods to y₁. The weights for periods 4 to 6 are the same as for period 3. The resulting closed-loop (servo) response is:

See Also
scmpc, smpccl, smpcsim

smpccl smpcest