

| GARCH Toolbox |   |
Equality Constraints and Parameter Significance
The GARCH Toolbox lets you set and constrain model parameters as a way of assessing the parameters' significance.
The Specification Structure Fix Fields
Each of the coefficient fields C, AR, MA, Regress, K, GARCH, and ARCH, in the specification structure, has a corresponding Boolean field that lets you hold any individual parameter fixed. These fix fields are FixC, FixAR, FixMA, FixRegress, FixK, FixGARCH, and FixARCH. For example, look at the output structure from the GARCH(2,1) estimation in the section Likelihood Ratio Tests.
coeff21 coeff21 = Comment: 'Mean: ARMAX(0,0,0); Variance: GARCH(2,1)' R: 0 M: 0 P: 2 Q: 1 Distribution: 'Gaussian' C: 4.9584e-004 AR: [] MA: [] Regress: [] K: 1.3645e-006 GARCH: [0.0358 0.9015] ARCH: 0.0538 FixC: [] FixAR: [] FixMA: [] FixRegress: [] FixK: [] FixGARCH: [] FixARCH: [] Optimization: [1x1 struct]
Each fix field, when not empty ([]), is the same size as the corresponding coefficient field. A 0 in a particular element of a fix field indicates that the corresponding element of its companion value field is an initial parameter guess that garchfit refines during the estimation process. A 1 indicates that garchfit holds the corresponding element of its value field fixed during the estimation process (i.e., an equality constraint).
The GARCH(2,1) Model as an Example
This example uses the GARCH(2,1) model above to demonstrate the use of equality constraints. First, display the estimation results for the model.
garchdisp(coeff21, errors21) Number of Parameters Estimated: 5 Standard T Parameter Value Error Statistic ----------- ----------- ------------ ----------- C 0.00049584 0.000256 1.9369 K 1.3645e-006 4.6186e-007 2.9545 GARCH(1) 0.0358 0.028327 1.2638 GARCH(2) 0.90149 0.029642 30.4131 ARCH(1) 0.05379 0.0073393 7.3291
The T-statistic column is the parameter value divided by the standard error, and is normally distributed for large samples. The T-statistic measures the number of standard deviations the parameter estimate is away from zero, and as a general rule, a T-statistic greater than 2 in magnitude corresponds to approximately a 95 percent confidence interval. The T-statistics in the table above imply that the conditional mean constant (C) is on the edge of significance. They also imply that the GARCH(1) parameter adds little if any explanatory power to the model.
The GARCH(1) Parameter. Constrain the GARCH(1) parameter at 0 to assess its significance.
specG1 = garchset(coeff21, 'GARCH', [0 0.9], 'FixGARCH', [1 0]) specG1 = Comment: 'Mean: ARMAX(0,0,?); Variance: GARCH(2,1)' R: 0 M: 0 P: 2 Q: 1 Distribution: 'Gaussian' C: 4.9584e-004 AR: [] MA: [] Regress: [] K: 1.3645e-006 GARCH: [0 0.9000] ARCH: 0.0538 FixC: [] FixAR: [] FixMA: [] FixRegress: [] FixK: [] FixGARCH: [1 0] FixARCH: [] Optimization: [1x1 struct]
The specG1 structure field FixGARCH indicates that garchfit holds GARCH(1) fixed at 0, and refines GARCH(2) from an initial value of 0.9 during the estimation process. In other words, the specG1 specification structure tests the composite model,
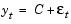
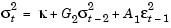
Now estimate the model subject to the equality constraint and display the results.
[coeffG1,errorsG1,LLFG1,innovationsG1,sigmaG1] = garchfit(specG1, xyz); garchdisp(coeffG1, errorsG1) Number of Parameters Estimated: 4 Standard T Parameter Value Error Statistic ----------- ----------- ------------ ----------- C 0.00052356 0.00025499 2.0532 K 1.6865e-006 4.6547e-007 3.6231 GARCH(1) 0 Fixed Fixed GARCH(2) 0.93442 0.0085294 109.5531 ARCH(1) 0.054718 0.0072265 7.5719 LLFG1 LLFG1 = 5.9738e+003
A more accurate value of LLFG1 is 5973.7872.
Notice that the standard error and T-statistic columns for the first GARCH parameter indicate that garchfit held the GARCH(1) parameter fixed. The number of estimated parameters also decreased from 5 in the original, unrestricted GARCH(2,1) model to 4 in this restricted GARCH(2,1) model.
Apply the likelihood ratio test as before.
[H, pValue, Stat, CriticalValue] = lratiotest(LLF21, LLFG1, 1, 0.05); [H pValue Stat CriticalValue] ans = 1.0000 0.0402 4.2112 3.8415
The results support rejection of the simpler, restricted model at the 0.05 significance level, but just barely. The P-value indicates that had you tested at a significance level of 0.04 or less, the restricted model would have been accepted.
The GARCH(2) Parameter. As a second example, assess the significance of the GARCH(2) parameter by setting it to 0.
specG2 = garchset(coeff21, 'GARCH', [0.9 0], 'FixGARCH', [0 1]) specG2 = Comment: 'Mean: ARMAX(0,0,?); Variance: GARCH(2,1)' R: 0 M: 0 P: 2 Q: 1 Distribution: 'Gaussian' C: 4.9584e-004 AR: [] MA: [] Regress: [] K: 1.3645e-006 GARCH: [0.9000 0] ARCH: 0.0538 FixC: [] FixAR: [] FixMA: [] FixRegress: [] FixK: [] FixGARCH: [0 1] FixARCH: [] Optimization: [1x1 struct]
The specG2 structure field FixGARCH indicates that garchfit holds GARCH(2) fixed at 0, and refines GARCH(1) from an initial value of 0.9 during the estimation process. In other words, the specG2 specification structure tests the composite model,
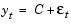
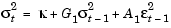
which is really the GARCH(1,1) default model.
Now, estimate the model subject to the equality constraint and display the results.
[coeffG2,errorsG2,LLFG2,innovationsG2,sigmaG2] = garchfit(specG2, xyz); garchdisp(coeffG2, errorsG2) Number of Parameters Estimated: 4 Standard T Parameter Value Error Statistic ----------- ----------- ------------ ----------- C 0.00048996 0.00025618 1.9126 K 7.9828e-007 2.6908e-007 2.9667 GARCH(1) 0.9636 0.0050784 189.7460 GARCH(2) 0 Fixed Fixed ARCH(1) 0.031239 0.0043564 7.1709 LLFG2 LLFG2 = 5.9746e+003
Note that a more accurate value of LLFG2 is 5974.6058.
Finally, apply the likelihood ratio test again,
[H, pValue, Stat, CriticalValue] = lratiotest(LLF21, LLFG2, 1, 0.05); [H pValue Stat CriticalValue] ans = 0 0.1086 2.5738 3.8415
In this case, the results support acceptance of the restricted model at the 0.05 significance level. In fact, the P-value indicates that the test would support acceptance at the 0.10 significance level as well. This result again emphasizes that the default GARCH(1,1) model adequately explains the variation in the observed returns. A close examination reveals that the log-likelihood function values of the two models are nearly identical (i.e., LLFG2 = 5974.6058, LLF11 = 5974.6025).
 | Akaike and Bayesian Information Criteria | Equality Constraints and Initial Parameter Estimates |  |