

| GARCH Toolbox |   |
Likelihood Ratio Tests
The section Analysis and Estimation Example Using the Default Model demonstrates that the default GARCH(1,1) model explains most of the variability of the returns of the XYZ Corporation. This example uses the function lratiotest to determine if evidence exists to support the use of a GARCH(2,1) model.
The example first fits the return series of the XYZ Corporation to the default GARCH(1,1) model. It then overfits the same series using the following, more elaborate, GARCH(2,1) model.
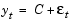
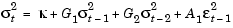
The example is presented in two parts:
Estimate Parameters for the GARCH(1,1) and GARCH(2,1) Models
The GARCH(1,1) Model. First, create a GARCH(1,1) default model with the Display flag set to off. Then, estimate the model and display the results, including the maximized log-likelihood function value.
spec11 = garchset('Display', 'off', 'P', 1, 'Q', 1); [coeff11, errors11, LLF11, innovations11, sigma11, summary11] = garchfit(spec11, xyz); garchdisp(coeff11, errors11) Number of Parameters Estimated: 4 Standard T Parameter Value Error Statistic ----------- ----------- ------------ ----------- C 0.00049183 0.00025585 1.9223 K 8.2736e-007 2.7446e-007 3.0145 GARCH(1) 0.96283 0.0051557 186.7500 ARCH(1) 0.03178 0.004416 7.1965 LLF11 LLF11 = 5.9746e+003
Note that a more accurate value of LLF11 is 5974.6025.
The GARCH(2,1) Model. Create a GARCH(2,1) specification structure. Again, set the Display flag to off.
spec21 = garchset('Display', 'off', 'P', 2, 'Q', 1) spec21 = Comment: 'Mean: ARMAX(0,0,?); Variance: GARCH(2,1)' R: 0 M: 0 P: 2 Q: 1 Distribution: 'Gaussian' C: [] AR: [] MA: [] Regress: [] K: [] GARCH: [] ARCH: [] FixC: [] FixAR: [] FixMA: [] FixRegress: [] FixK: [] FixGARCH: [] FixARCH: [] Optimization: [1x1 struct]
Now estimate the GARCH(2,1) model and display the results, including the maximized log-likelihood function value.
[coeff21,errors21,LLF21,innovations21,sigma21,summary21] = garchfit(spec21, xyz); garchdisp(coeff21, errors21) Number of Parameters Estimated: 5 Standard T Parameter Value Error Statistic ----------- ----------- ------------ ----------- C 0.00049584 0.000256 1.9369 K 1.3645e-006 4.6186e-007 2.9545 GARCH(1) 0.0358 0.028327 1.2638 GARCH(2) 0.90149 0.029642 30.4131 ARCH(1) 0.05379 0.0073393 7.3291 LLF21 LLF21 = 5.9759e+003
A more accurate value of LLF21 is 5975.8927.
Perform the Likelihood Ratio Test
Of the two models associated with the same return series:
Since garchfit enforces no boundary constraints during either of the two estimations, you can apply a likelihood ratio test (LRT) (see Hamilton [12], pages 142-144).
In this context, the unrestricted GARCH(2,1) model serves as the alternative hypothesis (i.e., the hypothesis the example gathers evidence to support), while the restricted GARCH(1,1) model serves as the null hypothesis (i.e., the hypothesis the example assumes is true, lacking any evidence to support the alternative).
The LRT statistic is asymptotically Chi-Square distributed with degrees-of-freedom equal to the number of restrictions imposed. Since the GARCH(1,1) model imposes one restriction, specify one degrees-of-freedom in your call to lratiotest. Test the models at the 0.05 significance level.
[H, pValue, Stat, CriticalValue] = lratiotest(LLF21, LLF11, 1, 0.05); [H pValue Stat CriticalValue] ans = 0 0.1082 2.5806 3.8415
H = 0 indicates that there is insufficient statistical evidence in support of the GARCH(2,1) model. The conclusion is that the default GARCH(1,1) model adequately explains the variability in the return series when compared to a more elaborate GARCH(2,1) model.
 | Model Selection and Analysis | Akaike and Bayesian Information Criteria |  |