GARCH Toolbox

Akaike and Bayesian Information Criteria

You can also use Akaike (AIC) and Bayesian (BIC) information criteria to compare alternative models. Since information criteria penalize models with additional parameters, the AIC and BIC model-order-selection criteria are based on parsimony (see Box, Jenkins, and Reinsel [7], pages 200-201).

The following example uses the default GARCH(1,1) and GARCH(2,1) models developed in the previous section, Likelihood Ratio Tests. It is presented in two parts:

• Counting Estimated Parameters
• Computing the AIC and BIC Criteria

Counting Estimated Parameters

For both AIC and BIC, you need to provide the number of parameters estimated in the model. For the relatively simple models in the previous example, you can just count the number of parameters. The GARCH(2,1) model estimated five parameters (C, 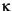, G₁, G₂, and A₁), and GARCH(1,1) model estimated four parameters (C, 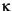, G₁, and A₁).

Use the function garchcount for more elaborate models. garchcount accepts the output specification structure created by garchfit and returns the number of parameters in the model defined in that structure.

• n21 = garchcount(coeff21)
  n21 =
       5
  n11 = garchcount(coeff11)
  n11 =
       4
  

Computing the AIC and BIC Criteria

Now use the function aicbic to compute the AIC and BIC statistics for the GARCH(2,1) model and the GARCH(1,1) model. Note that for the BIC statistic, you must also specify the number of observations in the return series.

• [AIC, BIC] = aicbic(LLF21, n21, 2000);
  [AIC   BIC]
  ans =
    1.0e+004 *
     -1.1942   -1.1914  
  

More accurate values are AIC = -11941.7855 and BIC = -11913.7810.

• 
  [AIC, BIC] = aicbic(LLF11, n11, 2000);
  [AIC   BIC]
  ans =
    1.0e+004 *
     -1.1941   -1.1919  
  

More accurate values are AIC = -11941.2049 and BIC = -11918.8013

You can use the relative values of the AIC and BIC statistics as guides in the model selection process. In this example, the AIC criterion favors the GARCH(2,1) model, while the BIC criterion favors the GARCH(1,1) default model with fewer parameters. Notice that since BIC imposes a greater penalty for additional parameters than does AIC, BIC always provides a model with a number of parameters no greater than that chosen by AIC.

Likelihood Ratio Tests

Equality Constraints and Parameter Significance