lratiotest (GARCH Toolbox)

Likelihood ratio hypothesis test

Syntax

[H, pValue, Ratio, CriticalValue] = lratiotest(BaseLLF, NullLLF, 
DoF, Alpha)

Arguments

BaseLLF
Scalar value of the optimized log-likelihood objective function of the baseline, unrestricted estimate. lratiotest assumes BaseLLF is the output of the estimation function garchfit, or the inference function garchinfer.

NullLLF
Vector of optimized log-likelihood objective function values of the restricted estimates. lratiotest assumes you obtained the NullLLF values using garchfit or garchinfer.

DoF
Degrees of freedom (i.e, the number of parameter restrictions) associated with each value in NullLLF. DoF can be a scalar applied to all values in NullLLF, or a vector the same length as NullLLF. All elements of DoF must be positive integers.

Alpha
(optional) Significance levels of the hypothesis test. Alpha can be a scalar applied to all values in NullLLF, or a vector the same length as NullLLF. If Alpha = [] or is not specified, the default is 0.05. For all elements, 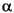, of Alpha, 0 < < 1.

`B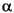aseLLF`	Scalar value of the optimized log-likelihood objective function of the baseline, unrestricted estimate. `lratiotest` assumes `BaseLLF` is the output of the estimation function `garchfit`, or the inference function `garchinfer`.
`NullLLF`	Vector of optimized log-likelihood objective function values of the restricted estimates. `lratiotest` assumes you obtained the `NullLLF` values using `garchfit` or `garchinfer`.
`DoF`	Degrees of freedom (i.e, the number of parameter restrictions) associated with each value in `NullLLF`. `DoF` can be a scalar applied to all values in `NullLLF`, or a vector the same length as `NullLLF`. All elements of `DoF` must be positive integers.
`Alpha`	(optional) Significance levels of the hypothesis test. `Alpha` can be a scalar applied to all values in `NullLLF`, or a vector the same length as `NullLLF`. If `Alpha = []` or is not specified, the default is `0.05`. For all elements, , of `Alpha`, `0` < `< 1`.

Description

[H, pValue, Ratio, CriticalValue] = lratiotest(BaseLLF, NullLLF, DoF, Alpha) performs the likelihood ratio hypothesis test. lratiotest uses as input the optimized log-likelihood objective function (LLF) value associated with an unrestricted maximum likelihood parameter estimate, and the LLF values associated with restricted parameter estimates.

The unrestricted LLF is the baseline case used to fit conditional mean and variance specifications to an observed univariate return series. The restricted models determine the null hypotheses of each test, and the number of restrictions they impose determines the degrees of freedom of the resulting Chi-Square distribution.

BaseLLF is usually the LLF of a larger estimated model and serves as the alternative hypothesis. Elements of NullLLF are then the LLFs associated with smaller, restricted specifications. BaseLLF should exceed the values in NullLLF, and the asymptotic distribution of the test statistic is Chi-Square distributed with degrees of freedom equal to the number of restrictions.

H
Vector of Boolean decisions the same size as NullLLF. A 0 indicates acceptance of the restricted model under the null hypothesis. 1 indicates rejection of the restricted, null hypothesis model relative to the unrestricted alternative associated with BaseLLF.

pValue
Vector of P-values (significance levels) at which lratiotest rejects the null hypothesis of each restricted model. pValue is the same size as NullLLF.

Ratio
Vector of likelihood ratio test statistics the same size as NullLLF. The test statistic is

CriticalValue
Vector of critical values of the Chi-Square distribution. CriticalValue is the same size as NullLLF.

`H`	Vector of Boolean decisions the same size as `NullLLF`. A `0` indicates acceptance of the restricted model under the null hypothesis. `1` indicates rejection of the restricted, null hypothesis model relative to the unrestricted alternative associated with `BaseLLF`.
`pValue`	Vector of P-values (significance levels) at which `lratiotest` rejects the null hypothesis of each restricted model. `pValue` is the same size as `NullLLF`.
`Ratio`	Vector of likelihood ratio test statistics the same size as `NullLLF`. The test statistic is
`CriticalValue`	Vector of critical values of the Chi-Square distribution. `CriticalValue` is the same size as `NullLLF`.

See Also
garchfit, garchinfer

Reference

[1] Hamilton, J.D., Time Series Analysis, Princeton University Press, 1994.

lbqtest parcorr