| GARCH Toolbox | |
Computing a Forecast
If the variables for the estimated model no longer exist in your workspace, then use the following commands to load the data and regenerate the estimation results of the default model. This example omits the estimation output to save space.
Using Default Inputs
Now call garchpred to compute the conditional mean and standard deviation return forecasts for the XYZ Corporation using the default model parameter estimates. Provide the specification structure coeff (the output of garchfit) and the XYZ Corporation return series xyz, as input. Accept the garchpred default (1) for the number of forecast periods.
The result consists of the MMSE forecasts of the conditional standard deviations and the conditional mean of the return series xyz for a one-period default horizon.
Note
garchpred allows the use of a time series regression matrix and an associated time series matrix of forecasted explanatory data. If you specify no regression matrix, the conditional mean has no regression component. See the section Conditional Mean Models with Regression Components for information about using regression models.
|
Forecasting Over a Longer Horizon
To obtain information about asymptotic behavior, you need to forecast for more more than a single period. Use the following command to forecast the conditional mean and standard deviation in each period of a 10-period forecast horizon.
[sFcast, yFcast] = garchpred(coeff, xyz, 10); [sFcast, yFcast] ans = 1.1670e-002 4.9183e-004 1.1674e-002 4.9183e-004 1.1678e-002 4.9183e-004 1.1682e-002 4.9183e-004 1.1686e-002 4.9183e-004 1.1690e-002 4.9183e-004 1.1694e-002 4.9183e-004 1.1697e-002 4.9183e-004 1.1701e-002 4.9183e-004 1.1705e-002 4.9183e-004
The results show that the default model forecast of the conditional mean is always C = 0.00049183. This is true for any forecast horizon because the expected value of any innovation,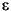 
t, is 0.
In contrast, the conditional standard deviation forecast changes from period to period and approaches the unconditional standard deviation of {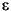t}, given by the square root of Eq. (2-7).
|
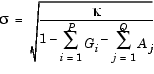
(2-17) |
For this example, you can calculate the unconditional standard deviation of {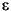t} as
Plot the conditional standard deviations, sigma, derived from the fitted returns. The plot reveals that the most recent values of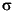 
t fall below this long-run, asymptotic value.
Figure 2-15: Fitted Conditional Standard Deviations
Long-Range Forecasting
That the most recent values of 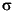t fall below 1.2393e-002 indicates that the long-range forecast of 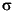t approaches this value from below. Confirm this by forecasting the standard deviations out 1000 periods, then plotting the forecasts (blue, dashed) and asymptotic value (red, solid) on the same graph.
sFcast = garchpred(coeff, xyz, 1000); plot(sFcast, 'blue--') hold('on') plot([0 length(sFcast)], [s0 s0], 'red') title('Standard Deviation Forecasts and Asymptotic Value: XYZ Corporation')
Figure 2-16: Standard Deviation Forecasts and Asymptotic Value
You can see from Figure 2-16, Standard Deviation Forecasts and Asymptotic Value that it takes a very long time for the forecast to reach its steady-state value. This is consistent with the high degree of persistence in the volatility process for the XYZ Corporation (see Figure 2-9, ACF of the Squared Returns).
Forecasting Returns Over Multiple Periods
In addition to computing conditional mean and volatility forecasts on a per-period basis, garchpred also computes volatility forecasts of returns for assets held for multiple periods. For example, to forecast the standard deviation of the return you would obtain if you purchased XYZ stock today and sold it 10 days from now,
[sFcast, yFcast, sTotal] = garchpred(coeff, xyz, 10); [sFcast, sTotal] ans = 1.1670e-002 1.1670e-002 1.1674e-002 1.6506e-002 1.1678e-002 2.0220e-002 1.1682e-002 2.3352e-002 1.1686e-002 2.6112e-002 1.1690e-002 2.8609e-002 1.1694e-002 3.0907e-002 1.1697e-002 3.3047e-002 1.1701e-002 3.5057e-002 1.1705e-002 3.6959e-002
The vector sTotal (the second column above) represents the standard deviation forecasts of returns when the asset is held for multiple periods. The first element contains the standard deviation of the return expected if XYZ stock were held for one period, the second element contains the standard deviation of the return expected if XYZ stock were held for two periods, and so on. The last element contains the volatility forecast of the expected return if XYZ were purchased today and held for 10 periods.
If you convert the standard deviations sFcast and sTotal to variances by squaring each element, you can see an interesting relationship between the cumulative sum of sFcast.^2 and sTotal.^2.
[cumsum(sFcast.^2) sTotal.^2] ans = 1.3618e-004 1.3618e-004 2.7246e-004 2.7246e-004 4.0883e-004 4.0883e-004 5.4530e-004 5.4530e-004 6.8185e-004 6.8185e-004 8.1850e-004 8.1850e-004 9.5524e-004 9.5524e-004 1.0921e-003 1.0921e-003 1.2290e-003 1.2290e-003 1.3660e-003 1.3660e-003
Although not exactly equivalent, this relationship in the presence of heteroscedasticity is similar to the familiar square-root-of-time rule for converting constant variances of uncorrelated returns expressed on a per-period basis to a variance over multiple periods. This relationship between sFcast and sTotal holds for the default conditional mean model only (i.e., the relationship is valid for uncorrelated returns).
Note that the calculation of sTotal is strictly correct for continuously compounded returns only, and is an approximation for periodically compounded returns.
Note
The sTotal output of garchpred is not available for conditional mean models with regression components.
|
| | Forecasting | Computing Root Mean Square Errors (RMSE) | |
