

| GARCH Toolbox |   |
Univariate GARCH process forecasting
Syntax
SigmaForecast = garchpred(Spec, Series, NumPeriods, X) [SigmaForecast, MeanForecast] = garchpred(Spec, Series, NumPeriods, X, XF) [SigmaForecast, MeanForecast, SigmaTotal, MeanRMSE] = garchpred(Spec, Series, NumPeriods)
Arguments
|
GARCH specification structure for the conditional mean and variance models. You can create Spec by calling the function garchset or the estimation function garchfit. |
|
Matrix of observations of the underlying univariate return series of interest for which garchpred generates forecasts. Each column of Series is an independent realization (i.e., path). The last row of Series holds the most recent observation of each realization. garchpred assumes that Series is a stationary stochastic process. It also assumes that the ARMA component of the conditional mean model (if any) is stationary and invertible. |
|
(optional) Positive, scalar integer representing the forecast horizon of interest. The value you specify should be compatible with the sampling frequency of Series. If NumPeriods = [] or is not specified, the default is 1. |
|
(optional) Time series regression matrix of observed explanatory data. Typically, X is a matrix of asset returns (e.g., the return series of an equity index), and represents the past history of the explanatory data. Each column of X is an individual time series used as an explanatory variable in the regression component of the conditional mean. In each column, the first row contains the oldest observation and the last row the most recent. The number of valid (non- NaN) most recent observations in each column of X must equal or exceed the number of valid most recent observations in Series. If the number of valid observations in a column of X exceeds that of Series, garchpred uses only the most recent observations of X. If X = [] or is not specified, the conditional mean (MeanForecast) has no regression component. |
XF |
(optional) Time series matrix of forecasted explanatory data. XF represents the evolution into the future of the same explanatory data found in X. Because of this, XF and X must have the same number of columns. In each column of XF, the first row contains the one-period-ahead forecast, the second row the two-period-ahead forecast, and so on.The number of rows (forecasts) in each column (time series) of XF must equal or exceed the forecast horizon NumPeriods. When the number of forecasts in XF exceeds NumPeriods, garchpred uses only the first NumPeriods forecasts. If XF = [] or is not specified, the conditional mean (MeanForecast) has no regression component. |
Description
garchpred forecasts the conditional mean and standard deviation of the univariate return series NumPeriods into the future, using specifications for the conditional mean and variance of an observed univariate return series as input. The conditional mean and variance can be of general ARMAX and GARCH form, respectively.
SigmaForecast = garchpred(Spec, Series, NumPeriods, X)
forecasts only the standard deviation of the univariate return series, Series. The regression matrix X is optional. If you specify XF, garchpred ignores it.
[SigmaForecast, MeanForecast] = garchpred(Spec, Series, NumPeriods,
X, XF)
forecasts both the conditional mean and standard deviation of the univariate return series, Series. X and XF are optional. However, for MeanForecast, if you specify X, you must also specify XF. For SigmaForecast, garchpred ignores XF.
[SigmaForecast, MeanForecast, SigmaTotal, MeanRMSE] =
garchpred(Spec, Series, NumPeriods)
in addition to forecasting the conditional mean and standard deviation of the univariate return series, computes the volatility forecasts of asset returns over multiperiod holding intervals, and the standard errors of conditional mean forecasts. If you compute SigmaTotal or MeanRMSE, SigmaForecast and MeanForecast can have no regression component.If you compute SigmaTotal or MeanRMSE, SigmaForecast and MeanForecast can have no regression component.
garchpred requires a complete conditional mean specification to correctly infer the innovations process that drives the forecasts. Because of this, you would typically use the same regression matrix of observed returns (X), if any, that you used for simulation (using garchsim) or estimation (using garchfit). XF, however, is just the forecast of X, and you only need it to forecast the conditional mean (MeanForecast). If you want to forecast only the conditional variance (SigmaForecast), XF is unnecessary.
|
Matrix of minimum mean square error (MSE) forecasts of the conditional standard deviations of Series on a per period basis. SigmaForecast has NumPeriods rows and the same number of columns as Series. The first row contains the one-period-ahead forecast for each realization of Series, the second row contains the two-period-ahead forecast, and so on. If a forecast horizon is > 1 (i.e., NumPeriods > 1), garchpred returns the per-period forecasts of all intermediate horizons, as well as the forecast at the specified horizon which is in the last row. |
|
Matrix of minimum MSE forecasts of the conditional mean of Series on a per-period basis. MeanForecast is the same size as SigmaForecast. The first row contains the forecast in the first period for each realization of Series, the second row contains the forecast in the second period, and so on. Both X and XF must be non-empty for MeanForecast to have a regression component. If X and XF are empty ([]) or not specified, MeanForecast is based on the ARMA model. If you specify X and XF, MeanForecast is based on the full ARMAX model. |
SigmaTotal |
Matrix of minimum mean square error (MSE) volatility forecasts of Series over multiperiod holding intervals. SigmaTotal is the same size as SigmaForecast. The first row contains the standard deviation of returns expected for assets held for one period for each realization of Series, the second row contains the standard deviation of returns expected for assets held for two periods, and so on. The last row contains the volatility forecast of the cumulative return obtained if an asset was held for the entire NumPeriods forecast horizon. garchpred computes the elements of SigmaTotal by taking the square root ofwhere s is the forecast horizon of interest ( NumPeriods), and 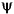 j is the coefficient of the jth lag of the innovations process in an infinite-order MA representation of the conditional mean model (see the function j is the coefficient of the jth lag of the innovations process in an infinite-order MA representation of the conditional mean model (see the function garchma). In the special case of the default model for the conditional mean, yt = C + 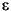 t, this reduces to t, this reduces toThe SigmaTotal forecasts are correct for continuously compounded returns, and approximate for periodically compounded returns. SigmaTotal is the same size as SigmaForecast if the conditional mean is modeled as a stationary invertible ARMA process. If you specify X or XF, SigmaTotal = []. |
|
Matrix of root mean square errors (RMSE) associated with MeanForecast. That is, MeanRMSE is the conditional standard deviation of the forecast errors (i.e., the standard error of the forecast) of the corresponding MeanForecast matrix. MeanRMSE is the same size as MeanForecast and garchpred organizes it in exactly the same manner, provided the conditional mean is modeled as a stationary/invertible ARMA process. If you specify X or XF, MeanRMSE = []. |
Note
garchpred calls the function garchinfer to access the past history of innovations and conditional standard deviations inferred from Series. If you need the innovations and conditional standard deviations, call garchinfer directly.
|
See Also
garchfit, garchinfer, garchma, garchset, garchsim
References
[1] Baillie, R.T., T. Bollerslev (1992), "Prediction in Dynamic Models with Time-Dependent Conditional Variances," Journal of Econometrics, Vol. 52, pp. 91-113.
[2] Bollerslev, T. (1986), "Generalized Autoregressive Conditional Heteroskedasticity," Journal of Econometrics, Vol. 31, pp. 307-327.
[3] Box, G.E.P., G.M. Jenkins, G.C. Reinsel, Time Series Analysis: Forecasting and Control, third edition, Prentice Hall, 1994.
[4] Engle, Robert (1982), "Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation," Econometrica, Vol. 50, pp. 987-1007.
[5] Hamilton, J.D., Time Series Analysis, Princeton University Press, 1994.
 | garchplot | garchset |  |