

| GARCH Toolbox |   |
A General Simulation Example
This simulation example is more general than the previous one that used the default model, GARCH(1,1). It uses an ARMA(2,1) model to express correlation in the conditional mean. The example:
Create the Model
Start by creating an ARMA(2,1)/GARCH(1,1) composite model with repeated calls to garchset.
spec = garchset; spec = garchset(spec, 'R', 2, 'M', 1); spec = garchset(spec, 'C', 0, 'AR', [0.6 0.2], 'MA', 0.4); spec = garchset(spec, 'K', 0.00001, 'GARCH', 0.8, 'ARCH', 0.1) spec = Comment: 'Mean: ARMAX(2,1,?); Variance: GARCH(1,1)' R: 2 M: 1 P: 1 Q: 1 Distribution: 'Gaussian' C: 0 AR: [0.6000 0.2000] MA: 0.4000 Regress: [] K: 1.0000e-005 GARCH: 0.8000 ARCH: 0.1000 FixC: [] FixAR: [] FixMA: [] FixRegress: [] FixK: [] FixGARCH: [] FixARCH: [] Optimization: [1x1 struct]
If you substitute the coefficient vectors from this specification structure in Eq. (2-8) and Eq. (2-9) you get the following ARMA(2,1) and GARCH(1,1) models. These are the models this example simulates.
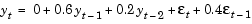
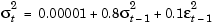
Simulate and Infer the Innovations
Use this model to simulate 2000 observations in a return series, and their corresponding innovations and standard deviations. Then use garchinfer to infer innovations and standard deviations from the simulated return series.
You can think of the simulation engine garchsim as a filter that generates a (possibly) correlated return series {yt} from a white noise input series {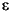 t}.
t}. garchinfer reverses this process by inferring innovations {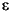 t} and standard deviation {
t} and standard deviation {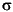 t} processes from the observations in {yt}.
t} processes from the observations in {yt}.
However, garchinfer is a convenience function that only provides a user-friendly interface to the log-likelihood objective function, garchllfn. So, in fact, garchllfn is the inverse (i.e., whitening) filter associated with the simulation engine, because it infers the white noise process from the observed return series. (See the section Understanding Transient Effects.)
Note
garchfit also calls the log-likelihood objective function, garchllfn, to infer the innovations and standard deviations.
|
Compare Simulated and Inferred Innovations
Now compare the simulated and inferred innovations for the first 20 observations. Notice that, after a few observations, the difference between the simulated and inferred innovations is insignificant.
eData = [[1:length(e)]' e eInferred [e-eInferred]]; fprintf('%4d %12.8f %12.8f %12.8f\n', eData(1:20,:)') 1 -0.00836573 0.00000000 -0.00836573 2 -0.01976087 0.00000000 -0.01976087 3 -0.00063568 -0.00854003 0.00790435 4 -0.01022288 -0.00706114 -0.00316174 5 0.00621509 0.00495039 0.00126470 6 0.00496725 0.00547313 -0.00050588 7 0.01596937 0.01576702 0.00020235 8 0.00610852 0.00618946 -0.00008094 9 -0.00640740 -0.00643977 0.00003238 10 0.00367566 0.00368861 -0.00001295 11 -0.00936189 -0.00936707 0.00000518 12 -0.00018263 -0.00018056 -0.00000207 13 -0.00043157 -0.00043240 0.00000083 14 0.00000037 0.00000070 -0.00000033 15 -0.00264566 -0.00264579 0.00000013 16 0.00890411 0.00890416 -0.00000005 17 -0.01577120 -0.01577122 0.00000002 18 0.00409658 0.00409659 -0.00000001 19 0.00825279 0.00825278 0.00000000 20 0.00672859 0.00672859 -0.00000000
In the example above, the difference between the simulated and inferred innovations (e - eInferred) illustrates the transient effects introduced by the inference. When garchsim generates data, it generates sufficient initial data, which it then discards, to allow transients to decay to some arbitrarily small value (see Automatic Minimization of Transient Effects). However, the inference function garchinfer (an interface to the log-likelihood objective function, garchllfn) must infer the innovations and conditional standard deviations directly from the observed returns. This can introduce transient effects.
That the first R = 2 rows of the inferred innovations are 0, illustrates the link between simulation, inference, and estimation in the GARCH Toolbox. This fact is also directly related to the manner in which maximum likelihood estimation is performed.
Maximum Likelihood Estimation
Forming the log-likelihood objective function involves a two-step process:
garchllfn uses the conditional mean specification of ARMAX form shown in Eq. (2-16) to infer the innovations from the observed returns. This equation is derived from Eq. (2-8) by solving for 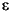 t.
t.
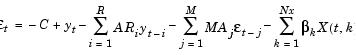
|
(2-16) |
garchllfn uses the Box and Jenkins conditional approach, which conditions the recursion on the initial R observations of yt, setting the initial values of 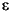 t to
t to 0 (see Hamilton [12], page 132, or Box, Jenkins, and Reinsel [7], page 237). Note that for the default model, R = M = 0, and no transients are induced due to this initialization.
garchllfn must then infer the conditional variances from the squared innovations as illustrated in Eq. (2-9), which is replicated here.
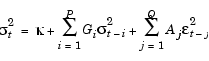
 t2 and
t2 and  t2 to the sample variance of the innovations inferred from the first step (see Hamilton [12], pages 666-667, or Bollerslev [4], page 316).
t2 to the sample variance of the innovations inferred from the first step (see Hamilton [12], pages 666-667, or Bollerslev [4], page 316).
 | Transients in the Simulation Process | Forecasting |  |