| GARCH Toolbox | |
Transients in the Simulation Process
Automatic Minimization of Transient Effects
The function garchsim generates stable output processes in (approximately) steady-state by attempting to eliminate transients in the data it simulates. garchsim first estimates the number of observations needed for the transients to decay to some arbitrarily small value, and then generates a number of observations equal to the sum of this estimated value and the number you request. garchsim then ignores the estimated number of initial samples needed for the transients to decay sufficiently and returns only the requested number of later observations.
To do this, garchsim interprets the simulated GARCH(P,Q) conditional variance process as an ARMA(max(P,Q),P) model for the squared innovations (see, for example, Bollerslev [4], p.310). It then interprets this ARMA(max(P,Q),P) model as the correlated output of a linear filter and estimates its impulse response by finding the magnitude of the largest eigenvalue of its auto-regressive polynomial. Based on this eigenvalue, garchsim estimates the number of observations needed for the magnitude of the impulse response (which begins at 1) to decay below 0.01 (i.e., 1 percent). If the conditional mean has an ARMA(R,M) component, then garchsim also estimates its impulse response.
Depending on the values of the parameters in the simulated conditional mean and variance models, you may need long pre-sample periods for the transients to die out. Although the simulation outputs may be relatively small matrices, the initial computation of these transients can result in a large memory burden and seriously impact performance. In the previous example, which simulates three 200-by-1000 element arrays, intermediate storage is required for far more than 200 observations.
Further Minimization of Transient Effects
If you suspect transients persist in the simulated data garchsim returns, you can oversample and delete observations from the beginning of each series. For example, suppose you would like to simulate 10 independent paths of 1000 observations each for {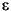
t}, {
t}, 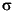and {yt} starting from a known scalar random number seed (12345). Start by generating 1200 observations, then further minimize the effect of transients by retaining only the last 1000 observations of interest.
[e,s,y] = garchsim(coeff, 1200, 10, 12345); whos e s y Name Size Bytes Class e 1200x10 96000 double array s 1200x10 96000 double array y 1200x10 96000 double array Grand total is 36000 elements using 288000 bytes e = e(end-999:end, :); s = s(end-999:end, :); y = y(end-999:end, :); whos e s y Name Size Bytes Class e 1000x10 80000 double array s 1000x10 80000 double array y 1000x10 80000 double array Grand total is 30000 elements using 240000 bytes
Note
The example above also illustrates how to specify a random number generator seed. If you do not specify a seed, as in the example in Simulating Multiple Paths, the default seed is 0 (the MATLAB initial state).
|
Understanding Transient Effects
The example in this section builds on the example in the section Further Minimization of Transient Effects. The previous example simulated 10 independent paths of 1000 observations each for {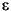t}, {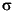t}, and {yt} and returned its outputs in the variables e, s, and y respectively. This example uses the GARCH Toolbox inference function garchinfer to infer {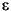t} and {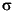t} from the simulated return series y. It then compares the steady-state simulated innovations and conditional standard deviation processes with the inferred innovations and conditional standard deviation processes.
Essentially, garchsim uses an ARMA model as a linear filter to transform an uncorrelated input innovations process {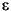t} into a correlated output returns process {yt}. Use the function garchinfer to reverse this process by inferring innovations {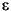t} and standard deviation {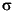t} processes from the observations in {yt}
where eInferred and sInferred are the inferred innovations and conditional standard deviations, respectively. Notice that when you query the workspace, eInferred and sInferred are the same size as the simulated returns matrix y
whos eInferred sInferred y Name Size Bytes Class eInferred 1000x10 80000 double array sInferred 1000x10 80000 double array y 1000x10 80000 double array Grand total is 30000 elements using 240000 bytes
Now compare the steady-state, simulated processes with their inferred counterparts by examining the third trial (i.e., the third column of each matrix). Note that there is nothing special about the third column, and the following comparisons hold for all columns.
First, create two matrices, eData and sData, to store the row numbers, the simulated and inferred series, and the difference between the two.
eData = [[1:length(e)]' e(:,3) eInferred(:,3) [e(:,3)-eInferred(:,3)]]; sData = [[1:length(s)]' s(:,3) sInferred(:,3) [s(:,3)-sInferred(:,3)]]; whos eData sData Name Size Bytes Class eData 1000x4 32000 double array sData 1000x4 32000 double array Grand total is 8000 elements using 64000 bytes
Now, print the first 10 rows of eData and sData, using the fprintf command to format the printed output, and examine the observations.
fprintf('%4d %12.8f %12.8f %12.8f\n', eData(1:10,:)') 1 -0.00111887 -0.00111887 0.00000000 2 -0.01022535 -0.01022535 0.00000000 3 -0.01391679 -0.01391679 0.00000000 4 0.00769383 0.00769383 0.00000000 5 0.00284161 0.00284161 0.00000000 6 0.00837156 0.00837156 0.00000000 7 -0.01022153 -0.01022153 0.00000000 8 -0.00064348 -0.00064348 0.00000000 9 0.00769471 0.00769471 0.00000000 10 -0.00011629 -0.00011629 -0.00000000 fprintf('%4d %12.8f %12.8f %12.8f\n', sData(1:10,:)') 1 0.01176309 0.01532522 -0.00356213 2 0.01157993 0.01506653 -0.00348661 3 0.01154388 0.01492360 -0.00337972 4 0.01163145 0.01488014 -0.00324869 5 0.01153130 0.01469346 -0.00316216 6 0.01136278 0.01445537 -0.00309258 7 0.01128578 0.01429146 -0.00300569 8 0.01125978 0.01417048 -0.00291070 9 0.01108652 0.01393485 -0.00284832 10 0.01100236 0.01377214 -0.00276979
Notice that the difference between the simulated and inferred innovations is effectively zero immediately, whereas the standard deviations appear to converge slowly. If you examine every 25th observation of the standard deviations, through the 400th observation, the convergence is more obvious.
fprintf('%4d %12.8f %12.8f %12.8f\n', sData(25:25:400,:)') 25 0.01060556 0.01230273 -0.00169717 50 0.01167755 0.01230644 -0.00062889 75 0.01290505 0.01312981 -0.00022476 100 0.01228385 0.01237591 -0.00009206 125 0.01256986 0.01260484 -0.00003498 150 0.01292421 0.01293742 -0.00001321 175 0.01212655 0.01213201 -0.00000546 200 0.01155697 0.01155919 -0.00000222 225 0.01409612 0.01409683 -0.00000071 250 0.01468410 0.01468437 -0.00000026 275 0.01336617 0.01336628 -0.00000011 300 0.01138117 0.01138123 -0.00000005 325 0.01414220 0.01414222 -0.00000002 350 0.01312882 0.01312883 -0.00000001 375 0.01494447 0.01494447 -0.00000000 400 0.01704352 0.01704352 -0.00000000
The innovations processes of the default model converge immediately because the default model assumes a simple constant in the conditional mean equation (i.e., there is no correlation in the conditional mean). However, the GARCH(1,1) default conditional variance equation is highly persistent (recall that the GARCH and ARCH parameter estimates are 0.9628 and 0.0318, respectively).
Note
The fprintf function lets you control the specific formatting of printed data. This example uses it to print the first 10 rows of eData and sData. It prints each innovation and difference value in fixed point notation, in a field of at least 12 digits, with 8 digits of precision. (See fprintf in the online MATLAB Function Reference.)
|
| | Simulating Sample Paths | A General Simulation Example | |