garchllfn (GARCH Toolbox)

Univariate GARCH process objective function (Gaussian innovations)

Syntax

[LogLikelihood, G, H, Innovations, Sigma] = garchllfn(Parameters, 
Series, R, M, P, Q, X)

Arguments

Parameters
Column vector of process parameters associated with fitting conditional mean and variance specifications to the observed return series, Series. The conditional mean contributes the first (1 + R + M + Nx) parameters, where Nx is the number of explanatory variables you include in the regression component of the conditional mean (the number of columns in X). The conditional variance contributes the remaining (1 + P + Q) parameters. The resultant length of Parameters is (2 + R + M + Nx + P + Q). (See the Formatting the Input Coefficient Vector section below.)

Series
Matrix of observations of the underlying univariate return series of interest for which garchllfn estimates the parameters of the conditional mean and variance models. Series can have several columns, where each column is an independent realization (i.e., path). The last row of Series holds the most recent observation of each realization.

R
Nonnegative, scalar integer representing the AR-process order.

M
Nonnegative, scalar integer representing the MA-process order.

P
Nonnegative, scalar integer representing the number of lags of the conditional variance included in the GARCH process.

Q
Nonnegative, scalar integer representing the number of lags of the squared innovations included in the GARCH process.

X
(optional) Time series regression matrix of observed explanatory data. Typically, X is a matrix of asset returns (e.g., the return series of an equity index), and represents the past history of the explanatory data. Each column of X is an individual time series used as an explanatory variable in the regression component of the conditional mean. In each column, the first row contains the oldest observation and the last row the most recent. X must have the same number of rows as Series.

`Parameters`	Column vector of process parameters associated with fitting conditional mean and variance specifications to the observed return series, `Series`. The conditional mean contributes the first (`1 + R + M + Nx`) parameters, where `Nx` is the number of explanatory variables you include in the regression component of the conditional mean (the number of columns in `X`). The conditional variance contributes the remaining (`1 + P + Q`) parameters. The resultant length of `Parameters` is (`2 + R + M + Nx + P + Q`). (See the Formatting the Input Coefficient Vector section below.)
`Series`	Matrix of observations of the underlying univariate return series of interest for which `garchllfn` estimates the parameters of the conditional mean and variance models. `Series` can have several columns, where each column is an independent realization (i.e., path). The last row of `Series` holds the most recent observation of each realization.
`R`	Nonnegative, scalar integer representing the AR-process order.
`M`	Nonnegative, scalar integer representing the MA-process order.
`P`	Nonnegative, scalar integer representing the number of lags of the conditional variance included in the GARCH process.
`Q`	Nonnegative, scalar integer representing the number of lags of the squared innovations included in the GARCH process.
`X`	(optional) Time series regression matrix of observed explanatory data. Typically, `X` is a matrix of asset returns (e.g., the return series of an equity index), and represents the past history of the explanatory data. Each column of `X` is an individual time series used as an explanatory variable in the regression component of the conditional mean. In each column, the first row contains the oldest observation and the last row the most recent. `X` must have the same number of rows as `Series`.

Description

[LogLikelihood, G, H, Innovations, Sigma] = garchllfn(Parameters, Series, R, M, P, Q, X) computes the log-likelihood objective function value suitable for maximum likelihood estimation (MLE).

For Gaussian innovations, garchfit uses garchllfn as the objective function to be optimized by fmincon. When garchinfer calls garchllfn, the primary outputs of garchllfn are the innovations and conditional standard deviations inferred from the input data. In either case, garchllfn must infer an uncorrelated white noise innovation process. In this sense, garchllfn is an inverse, or whitening, filter.

The use of garchllfn is specific to Distribution = 'Gaussian' in the GARCH specification structure.

Note Because garchllfn is performance sensitive and because fmincon calls it iteratively as the objective function, garchllfn performs no argument checking. Although you can call garchllfn directly, it is better to call it via garchinfer.

LogLikelihood
Vector of log-likelihood objective function values evaluated at the values in Parameters. The length of LogLikelihood is the same as the number of columns in Series. Because the fmincon function (of the Optimization Toolbox), which is used to optimize garchllfn, is a minimization routine, LogLikelihood is the negative of what is formally presented in most econometrics references

G
Reserved for future use. G = [].

H
Reserved for future use. H = [].

Innovations
Innovations matrix inferred from the input Series matrix.

Sigma
Conditional standard deviation matrix corresponding to Innovations.

`LogLikelihood`	Vector of log-likelihood objective function values evaluated at the values in `Parameters`. The length of `LogLikelihood` is the same as the number of columns in `Series`. Because the `fmincon` function (of the Optimization Toolbox), which is used to optimize `garchllfn`, is a minimization routine, `LogLikelihood` is the negative of what is formally presented in most econometrics references
`G`	Reserved for future use. `G = []`.
`H`	Reserved for future use. `H = []`.
`Innovations`	Innovations matrix inferred from the input `Series` matrix.
`Sigma`	Conditional standard deviation matrix corresponding to `Innovations`.

Formatting the Input Coefficient Vector

Format the input coefficient vector Parameters exactly as you would read the coefficients from the recursive difference equations when solving for the current values of the y_t and 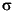_t² time series. Specifically, if:

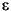y_t = return series of interest (assumed stationary)
_t = innovations of the model noise process (assumed invertible)
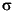_t² = conditional variance of the innovations process 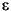_t

then the following equations represent the general ARMAX(R,M,Nx)/GARCH(P,Q) model.

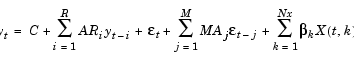
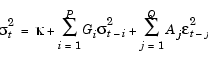
You can also write these equations as

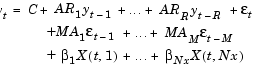
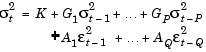
Using this form, the following equations represent the conditional mean and variance of a specific ARMAX(R=2, M=2, Nx=1) / GARCH(P=2, Q=2) composite model.

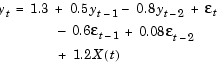
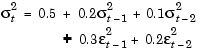
In the MATLAB notation, and using specification structure parameter names, the coefficient vector, Parameters, that represents this model is

Parameters =
 [ C     AR(1:R)   MA(1:M)     B(1:Nx)  K     GARCH(1:P)  ARCH(1:Q) ]' =
 [ 1.3   0.5 -0.8  -0.6 0.08   1.2      0.5   0.2 0.1     0.3 0.2   ]'

Note that the coefficient of 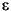_t in the conditional mean equation is 1. Since garchfit does not estimate the coefficient of 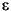_t, the coefficient vector does not include it.

Inferring the Innovations

garchllfn uses the following conditional mean specification of ARMAX form to infer the innovations, and then fits the conditional variance of the innovations to a GARCH model. It assumes Gaussian innovations.

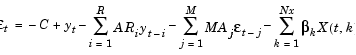
You can derive this equation from the general conditional mean equation given above for y_t, by solving it for 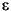_t. Its coefficient vector, which garchllfn uses to infer the innovations, is the negation of Parameters with the insertion of the y_t coefficient.

See Maximum Likelihood Estimation for more information.

See Also
garchfit, garchinfer, garchpred, garchsim

References

Bollerslev, T. (1986), "Generalized Autoregressive Conditional Heteroskedasticity," Journal of Econometrics, Vol. 31, pp. 307-327.

Box, G.E.P., G.M. Jenkins, G.C. Reinsel, Time Series Analysis: Forecasting and Control, third edition, Prentice Hall, 1994.

Engle, Robert (1982), "Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation," Econometrica, Vol. 50, pp. 987-1007.

Hamilton, J.D., Time Series Analysis, Princeton University Press, 1994.

garchinfer garchma