GARCH Toolbox

parcorr

Plot or return computed sample partial auto-correlation function

Syntax

• [PartialACF, Lags, Bounds] = parcorr(Series, nLags, R, nSTDs)
  

Arguments

Series	Vector of observations of a univariate time series for which parcorr returns or plots the sample partial auto-correlation function (partial ACF). The last element of Series contains the most recent observation of the stochastic sequence.
nLags	(optional) Positive, scalar integer indicating the number of lags of the partial ACF to compute. If nLags = [] or is not specified, parcorr computes the partial ACF sequence at lags 0, 1, 2, ..., T, where T = min([20, length(Series)-1]).
R	(optional) Nonnegative integer scalar indicating the number of lags beyond which parcorr assumes the theoretical partial ACF is zero. Assuming that Series is an AR(R) process, the estimated partial ACF coefficients at lags > R are approximately zero-mean, independently distributed Gaussian variates. In this case, the standard error of the estimated partial ACF coefficients of a fitted Series with N observations is approximately 1 / 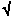N for lags > R. If R = [] or is not specified, the default is 0. The value of R must be < nLags.
nSTDs	(optional) Positive scalar indicating the number of standard deviations of the sample partial ACF estimation error to display, assuming that Series is an AR(R) process. If the Rth regression coefficient (i.e., the last ordinary least squares (OLS) regression coefficient of Series regressed on a constant and R of its lags) includes N observations, specifying nSTDs results in confidence bounds at ±(nSTDs / 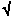N). If nSTDs = [] or is not specified, the default is 2 (i.e., approximate 95 percent confidence interval).

Description

parcorr(Series, nLags, R, nSTDs) computes and plots the sample partial auto-correlation function (partial ACF) of a univariate, stochastic time series. parcorr computes the partial ACF by fitting successive autoregressive models of orders 1, 2, ... by ordinary least squares, retaining the last coefficient of each regression. To plot the partial ACF sequence without the confidence bounds, set nSTDs = 0.

[PartialACF, Lags, Bounds] = parcorr(Series, nLags, R, nSTDs) computes and returns the partial ACF sequence.

PartialACF	Sample partial ACF of Series. PartialACF is a vector of length nLags + 1 corresponding to lags 0, 1, 2, ..., nLags. The first element of PartialACF is unity, i.e., PartialACF(1) = 1 = OLS regression coefficient of Series regressed upon itself. parcorr includes this element as a reference.
Lags	Vector of lags corresponding to PartialACF(0, 1, 2, ..., nLags).
Bounds	Two-element vector indicating the approximate upper and lower confidence bounds, assuming that Series is an AR(R) process. Note that Bounds is approximate for lags > R only.

Example

Create a stationary AR(2) process from a sequence of 1000 Gaussian deviates, and then visually assess whether the partial ACF is zero for lags > 2.

• randn('state',0)                % Start from a known state.
  x = randn(1000,1);              % 1000 Gaussian deviates ~ N(0,1).
  y = filter(1,[1 -0.6 0.08],x);  % Create a stationary AR(2)
                                  % process.
  [PartialACF, Lags, Bounds] = parcorr(y , [] , 2); % Compute the
                                  % partial ACF with 95 percent
                                  % confidence.
  [Lags, PartialACF]
  
  ans =
  
           0    1.0000
      1.0000    0.5570
      2.0000   -0.0931
      3.0000    0.0249
      4.0000   -0.0180
      5.0000   -0.0099
      6.0000    0.0483
      7.0000    0.0058
      8.0000    0.0354
      9.0000    0.0623
     10.0000    0.0052
     11.0000   -0.0109
     12.0000    0.0421
     13.0000   -0.0086
     14.0000   -0.0324
     15.0000    0.0482
     16.0000    0.0008
     17.0000   -0.0192
     18.0000    0.0348
     19.0000   -0.0320
     20.0000    0.0062
  
  Bounds
  
  Bounds =
  
      0.0633
     -0.0633
  
  parcorr(y , [] , 2)            % Use the same example, but plot
                                 % the partial ACF sequence with
                                 % confidence bounds.
  
  
  

See Also
autocorr, crosscorr

filter (in the online MATLAB Function Reference)

References

[1]  Box, G.E.P., G.M. Jenkins, G.C. Reinsel, Time Series Analysis: Forecasting and Control, third edition, Prentice Hall, 1994.

[2]  Hamilton, J.D., Time Series Analysis, Princeton University Press, 1994.

lratiotest

price2ret