GARCH Toolbox

autocorr

Plot or return computed sample auto-correlation function

Syntax

• autocorr(Series, nLags, M, nSTDs)
  [ACF, Lags, Bounds] = autocorr(Series, nLags, M, nSTDs)
  

Arguments

Series	Vector of observations of a univariate time series for which autocorr computes or plots the sample auto-correlation function (ACF). The last element of Series contains the most recent observation of the stochastic sequence.
nLags	(optional) Positive, scalar integer indicating the number of lags of the ACF to compute. If nLags = [] or is not specified, the default is to compute the ACF at lags 0, 1, 2, ..., T, where T = min([20, length(Series)-1]).
M	(optional) Nonnegative integer scalar indicating the number of lags beyond which the theoretical ACF is effectively 0. autocorr assumes the underlying Series is an MA(M) process, and uses Bartlett's approximation to compute the large-lag standard error for lags > M. If M = [] or is not specified, the default is 0, and autocorr assumes that Series is Gaussian white noise. If Series is a Gaussian white noise process of length N, the standard error is approximately 1 / 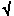N. M must be < nLags.
nSTDs	(optional) Positive scalar indicating the number of standard deviations of the sample ACF estimation error to compute. autocorr assumes the theoretical ACF of Series is 0 beyond lag M. When M = 0 and Series is a Gaussian white noise process of length N, specifying nSTDs results in confidence bounds at ±(nSTDs / 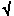N). If nSTDs = [] or is not specified, the default is 2 (i.e., approximate 95 percent confidence interval).

Description

autocorr(Series, nLags, M, nSTDs) computes and plots the sample ACF of a univariate, stochastic time series with confidence bounds. To plot the ACF sequence without the confidence bounds, set nSTDs = 0.

[ACF, Lags, Bounds] = autocorr(Series, nLags, M, nSTDs) computes and returns the ACF sequence.

ACF	Sample auto-correlation function of Series. ACF is a vector of length nLags+1 corresponding to lags 0, 1, 2, ..., nLags. The first element of ACF is unity, that is, ACF(1) = 1 = lag 0 correlation.
Lags	Vector of lags corresponding to ACF(0,1,2,...,nLags). Since an ACF is symmetric about 0 lag, autocorr ignores negative lags.
Bounds	Two element vector indicating the approximate upper and lower confidence bounds, assuming that Series is an MA(M) process. Values of ACF beyond lag M that are effectively 0 lie within these bounds. Note that autocorr computes Bounds only for lags > M.

Example

Create an MA(2) process from a sequence of 1000 Gaussian deviates, and assess whether the ACF is effectively zero for lags > 2.

• randn('state', 0)             % Start from a known state.
  x = randn(1000, 1);           % 1000 Gaussian deviates ~ N(0,1).
  y = filter([1 -1 1], 1, x);   % Create an MA(2) process.
  [ACF, Lags, Bounds] = autocorr(y, [], 2);  % Compute the ACF
                                             % with 95 percent 
                                             % confidence.
  [Lags, ACF]
  
  ans =
  
           0    1.0000
      1.0000   -0.6487
      2.0000    0.3001
      3.0000    0.0229
      4.0000    0.0196
      5.0000   -0.0489
      6.0000    0.0452
      7.0000    0.0012
      8.0000   -0.0214
      9.0000    0.0235
     10.0000    0.0340
     11.0000   -0.0392
     12.0000    0.0188
     13.0000    0.0504
     14.0000   -0.0600
     15.0000    0.0251
     16.0000    0.0441
     17.0000   -0.0732
     18.0000    0.0755
     19.0000   -0.0571
     20.0000    0.0485
  
  Bounds =
  
      0.0899
     -0.0899
  
  autocorr(y, [], 2)      % Use the same example, but plot the ACF
                          % sequence with confidence bounds.
  
   
  
  
  
  

See Also
crosscorr, parcorr

filter (in the online MATLAB Function Reference)

Reference

[1]  Box, G.E.P., G.M. Jenkins, G.C. Reinsel, Time Series Analysis: Forecasting and Control, third edition, Prentice Hall, 1994.

[2]  Hamilton, J.D., Time Series Analysis, Princeton University Press, 1994.

archtest

crosscorr