GARCH Toolbox

garchar

Convert finite-order ARMA models to infinite-order auto-regressive (AR) models

Syntax

• InfiniteAR  = garchar(AR, MA, NumLags)
  

Arguments

AR	R-element vector of auto-regressive coefficients associated with the lagged observations of a univariate return series modeled as a finite order, stationary, invertible ARMA(R,M) model.
MA	M-element vector of moving-average coefficients associated with the lagged innovations of a finite-order, stationary, invertible univariate ARMA(R,M) model.
NumLags	(optional) Number of lagged AR coefficients that garchar includes in the approximation of the infinite-order AR representation. NumLags is an integer scalar and determines the length of the infinite-order AR output vector. If NumLags = [] or is not specified, the default is 10.

Description

InfiniteAR = garchar(AR, MA, NumLags) computes the coefficients of an infinite-order AR model, using the coefficients of the equivalent univariate, stationary, invertible, finite-order ARMA(R,M) model as input. garchar truncates the infinite-order AR coefficients to accommodate a user-specified number of lagged AR coefficients.

InfiniteAR

Vector of coefficients of the infinite-order AR representation associated with the finite-order ARMA model specified by the AR and MA input vectors. InfiniteAR is a vector of length NumLags. The jth element of InfiniteAR is the coefficient of the jth lag of the input series in an infinite-order AR representation. Note that Box, Jenkins, and Reinsel refer to the infinite-order AR coefficients as " weights."

In the following ARMA(R,M) model, {y_t} is the return series of interest and {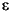_t} the innovations noise process.

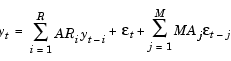
If you write this model equation as

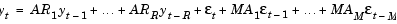
you can specify the garchar input coefficient vectors, AR and MA, exactly as you read them from the model. In general, the jth elements of AR and MA are the coefficients of the jth lag of the return series and innovations processes y_{t - j} and 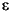_{t - j}, respectively. garchar assumes that the current-time-index coefficients of y_t and 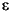_t are 1 and are not part of AR and MA.

In theory, you can use the 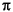weights returned in InfiniteAR, to approximate y_t as a pure AR process.

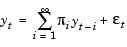
Consistently, the jth element of the truncated infinite-order auto-regressive output vect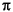or, _j or InfiniteAR(j), is the coefficient of the jth lag of the observed return series, y_{t - j}, in this equation. See Box, Jenkins, and Reinsel [7], Section 4.2.3, pages 106-109.

Given the above discussion, the AR and MA vectors differ from the corresponding AR and MA polynomials formally presented in time series references such as Box, Jenkins, and Reinsel. The conversion from GARCH Toolbox vectors to the corresponding GARCH Toolbox polynomials is:

• AR polynomial tested for stationarity = [1 ; -AR]
  MA polynomial tested for invertibility = [1 ; MA]
  

Example

For the following ARMA(2,2) model, use garchar to obtain the first 20 weights of the infinite order AR approximation.

From this model,

• AR = [0.5 -0.8] 
  MA = [-0.6 0.08]
  

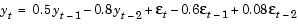
Since the current-time-index coefficients of y_t and _t are defined to be 1, the example omits them from AR and MA. This saves time and effort when you specify parameters using the garchset and garchget interfaces.

• PI = garchar([0.5 -0.8], [-0.6 0.08], 20);
  
  PI'
  
  ans =
  
     -0.1000
     -0.7800
     -0.4600
     -0.2136
     -0.0914
     -0.0377
     -0.0153
     -0.0062
     -0.0025
     -0.0010
     -0.0004
     -0.0002
     -0.0001
     -0.0000
     -0.0000
     -0.0000
     -0.0000
     -0.0000
     -0.0000
     -0.0000
  

See Also
garchfit, garchma, garchpred

Reference

[1]  Box, G.E.P., G.M. Jenkins, G.C. Reinsel, Time Series Analysis: Forecasting and Control, third edition, Prentice Hall, 1994.

crosscorr

garchcount