FFT (DSP Blockset)

Compute the FFT of the input.

Library

Description

The FFT block computes the fast Fourier transform (FFT) of each channel in the M-by-N or length-M input, u, where M must be a power of two. To work with other input sizes, use the Zero Pad block to pad or truncate the length-M dimension to a power-of-two length. The output is always complex-valued and sample-based (it is an unoriented 1-D vector for unoriented inputs).

y = fft(u,M)         % Equivalent MATLAB code

The kth entry of the lth output channel, y(k, l), is the kth point of the M-point discrete Fourier transform (DFT) of the lth input channel.

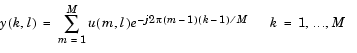
(7-2)

For information on block output characteristics and how to configure the block computation methods, see other sections of this reference page.

Sections of This Reference Page

Input and Output Characteristics

The following table describes all valid block input types, their corresponding outputs, and the dimension along which the block computes the DFT.

Note For M-by-N and length-M inputs, M must be a power of two. To work with other input sizes, use the Zero Pad block to pad or truncate the length-M dimension to a power-of-two length. Also, to get valid outputs, your inputs must be in linear order.

Valid Block Inputs
Real- or complex-valued

Must be in linear order

M must be a power of two

Dimension Along Which Block Computes DFT
Corresponding Block Output Characteristics
Output port rate = input port rate

Frame-based M-by-N matrix
Column

Sample-based

Complex-valued

Same dimensions as input

Each column (each row for sample-based row inputs) contains the M-point DFT of the corresponding input channel in linear or bit-reversed order.

Sample-based M-by-N matrix,
Column

Sample-based 1-by-M row vector
Row

Unoriented length-M 1-D vector
Vector
Unoriented, length-M, complex-valued 1-D vector containing M-point DFT of input in linear or bit-reversed order

Valid Block Inputs Real- or complex-valued Must be in linear order M must be a power of two	Dimension Along Which Block Computes DFT	Corresponding Block Output Characteristics Output port rate = input port rate
Frame-based M-by-N matrix	Column	Sample-based Complex-valued Same dimensions as input Each column (each row for sample-based row inputs) contains the M-point DFT of the corresponding input channel in linear or bit-reversed order.
Sample-based M-by-N matrix,	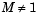Column
Sample-based 1-by-M row vector	Row
Unoriented length-M 1-D vector	Vector	Unoriented, length-M, complex-valued 1-D vector containing M-point DFT of input in linear or bit-reversed order

Click here in the MATLAB Help Browser to open a Simulink model based on the following diagram.

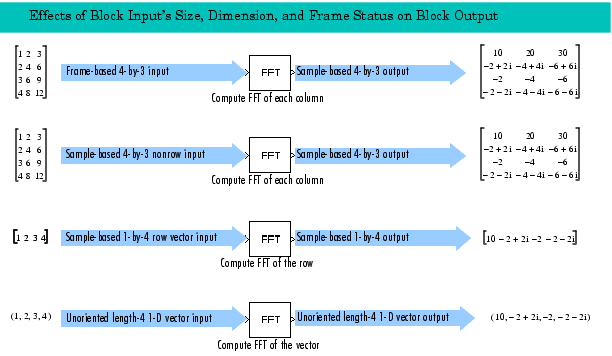
Ordering Output Column Entries (Output in bit-reversed order Parameter)

Set the Output in bit-reversed order parameter as follows to indicate the ordering of the output's column elements. For a definition of bit-reversed ordering, see Description of Bit-Reversed Ordering.

Parameter Setting
Ordering of Output Channel Elements
Output Column Entries

Linear order
(See the following note.)
kth column element is the DFT of the corresponding input column at the kth frequency.

Bit-reversed order
kth column element is the DFT of the corresponding input column at the rth frequency, where r is the bit reversed value of k.

Parameter Setting	Ordering of Output Channel Elements	Output Column Entries
	Linear order (See the following note.)	kth column element is the DFT of the corresponding input column at the kth frequency.
	Bit-reversed order	kth column element is the DFT of the corresponding input column at the rth frequency, where r is the bit reversed value of k.

Note Linearly ordering the output requires extra data sorting manipulation, so in some situations it may be better to output in bit-reversed order as illustrated in the example, Use of Outputs in Bit-Reversed Order.

The next diagram illustrates the difference between linear and bit-reversed outputs. Note that output values in linear and bit-reversed order are the same; only the order in which they appear in the columns differs.

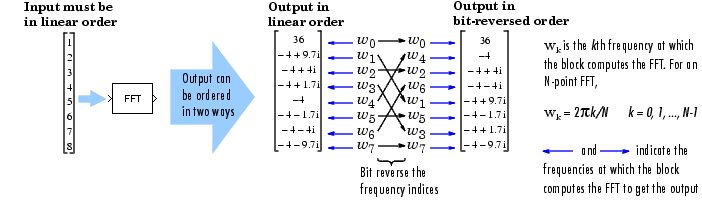
Description of Bit-Reversed Ordering. Two numbers are bit-reversed values of each other when the binary representation of one is the mirror image of the binary representation of the other. For example, in a three-bit system, one and four are bit-reversed values of each other, since the three-bit binary representation of one, 001, is the mirror image of the three-bit binary representation of four, 100.

The sequence 0, 1, 2, 3, 4, 5, 6, 7, is in linear order. To put the sequence in bit-reversed order, replace each element in the linearly ordered sequence with its bit-reversed counterpart. You can do this by translating the sequence into its binary representation (with the minimum number of bits), then finding the mirror image of each binary entry, and translating the sequence back to its decimal representation. The resulting sequence is the original linearly ordered sequence in bit-reversed order.

Selecting the Twiddle Factor Computation Method

The Twiddle factor computation parameter determines how the block computes the necessary sine and cosine terms to calculate the term 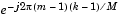in Equation 7-2. This parameter has two settings, each with its advantages and disadvantages, as described in the following table.

Twiddle factor computation Parameter Setting
Sine and Cosine Computation Method
Effect on Block Performance

Table lookup
The block computes and stores the trigonometric values before the simulation starts, and retrieves them during the simulation. When you generate code from the block, the processor running the generated code stores the trigonometric values computed by the block, and retrieves the values during code execution.
The block usually runs much more quickly, but requires extra memory for storing the precomputed trigonometric values. You can optimize the table for memory consumption or speed, as described in Optimizing the Table of Trigonometric Values below.

Trigonometric fcn
The block computes sine and cosine values during the simulation. When you generate code from the block, the processor running the generated code computes the sine and cosine values while the code runs.
The block usually runs more slowly, but does not need extra data memory. For code generation, the block requires a support library to emulate the trigonometric functions, increasing the size of the generated code.

Twiddle factor computation Parameter Setting	Sine and Cosine Computation Method	Effect on Block Performance
Table lookup	The block computes and stores the trigonometric values before the simulation starts, and retrieves them during the simulation. When you generate code from the block, the processor running the generated code stores the trigonometric values computed by the block, and retrieves the values during code execution.	The block usually runs much more quickly, but requires extra memory for storing the precomputed trigonometric values. You can optimize the table for memory consumption or speed, as described in Optimizing the Table of Trigonometric Values below.
Trigonometric fcn	The block computes sine and cosine values during the simulation. When you generate code from the block, the processor running the generated code computes the sine and cosine values while the code runs.	The block usually runs more slowly, but does not need extra data memory. For code generation, the block requires a support library to emulate the trigonometric functions, increasing the size of the generated code.

Optimizing the Table of Trigonometric Values

When you set the Twiddle factor computation parameter to Table lookup, you need to set the Optimize table for parameter. This parameter optimizes the table of trigonometric values for speed or memory by varying the number of table entries as summarized in the following table.

Optimize table for Parameter Setting
Number of Table Entries for N-Point FFT
Memory Required for Single-Precision 512-Point FFT

Speed
3N/4
1536 bytes

Memory
N/4 + 1
516 bytes

Optimize table for Parameter Setting	Number of Table Entries for N-Point FFT	Memory Required for Single-Precision 512-Point FFT
Speed	3N/4	1536 bytes
Memory	N/4 + 1	516 bytes

Algorithms Used for FFT Computation

Depending on whether the block input is real- or complex-valued, and whether you want the output in linear or bit-reversed order, the block uses one or more of the following algorithms as summarized in the next table:

Radix-2 decimation-in-time (DIT) algorithm
Radix-2 decimation-in-frequency (DIF) algorithm
Half-length algorithm

Double-signal algorithm


Input Complexity	Output Ordering	Algorithms Used for FFT Computation
Complex	Linear or bit-reversed	Radix-2 DIT
Real	Linear	Radix-2 DIT in conjunction with the half-length and double-signal algorithms when possible
Real	Bit-reversed	Radix-2 DIF in conjunction with the half-length and double-signal algorithms when possible

Example

Use of Outputs in Bit-Reversed Order. The FFT block runs more quickly when it outputs in bit-reversed order. You can often use an output in bit-reversed order when your model also uses the IFFT block (the IFFT block allows you to indicate whether its input is in bit-reversed or linear order). For instance, set the FFT block to output in bit-reversed order when you want to filter or convolve signals by taking the FFT of time domain data, multiplying frequency-domain data, and inputting the product to an IFFT block.

The following model shows the implementation of the Overlap-Save FFT Filter block. The implementation uses the FFT block in conjunction with an IFFT block, so the FFT block is set to output in bit-reversed order, and the IFFT block is set to accept inputs in bit-reversed order. Note the implementation uses the bitrevorder function to put the vector H into bit-reversed order before multiplying it with the bit-reversed FFT outputs.

Click here in the MATLAB Help browser to open the demo model. Alternatively, type the following command at the MATLAB command line.

olapfilt             % Open the following demo model

To see the implementation of the Overlap-Save FFT Filter block, right-click on the Overlap-Save FFT Filter block, and select Look under mask.
Look under the mask of the Overlap-Add FFT Filter block as well, which also uses an FFT block that outputs in bit-reversed order.

Dialog Box

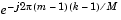Twiddle factor computation: Computation method of the term in Equation 7-2. In Table lookup mode, the block computes and stores the sine and cosine values before the simulation starts. In Trigonometric fcn mode, the block computes the sine and cosine values during the simulation. See Selecting the Twiddle Factor Computation Method.
Optimize table for: Optimization of the table of sine and cosine values for Speed or Memory. Active only when Twiddle factor computation is set to Table lookup. See Selecting the Twiddle Factor Computation Method.
Output in bit-reverse order: Order of the output channel elements relative to the ordering of the input elements. When checked, the output channel elements are in bit-reversed order relative to the input ordering. Otherwise, the output column elements are linearly ordered relative to the input ordering. See Ordering Output Column Entries (Output in bit-reversed order Parameter).

Supported Data Types

Double-precision floating point
Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Complex Cepstrum
DSP Blockset

DCT
DSP Blockset

IFFT
DSP Blockset

Pad
DSP Blockset

Zero Pad
DSP Blockset

bitrevorder
Signal Processing Toolbox

fft
Signal Processing Toolbox

ifft
Signal Processing Toolbox

Complex Cepstrum	DSP Blockset
DCT	DSP Blockset
IFFT	DSP Blockset
Pad	DSP Blockset
Zero Pad	DSP Blockset
`bitrevorder`	Signal Processing Toolbox
`fft`	Signal Processing Toolbox
`ifft`	Signal Processing Toolbox

Also see Transforms for a list of all the blocks in the Transforms library.

Extract Triangular Matrix Filter Realization Wizard