IFFT (DSP Blockset)

Compute the IFFT of the input.

Library

Description

The IFFT block computes the inverse fast Fourier transform (IFFT) of each channel in the M-by-N or length-M input, u, where M must be a power of two. To work with other input sizes, use the Zero Pad block to pad or truncate the length-M dimension to a power-of-two length. The output is always frame-based, and each output column contains the M-point inverse discrete Fourier transform (IDFT) of the corresponding input channel.

y = ifft(u,M)        % Equivalent MATLAB code

The kth entry of the lth output channel, y(k, l), is the kth point of the M-point IDFT of the lth input channel.

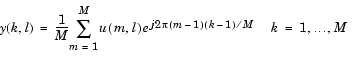
(7-3)

You can choose to output a scaled version of the input's IDFT, 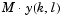, by setting the parameter Skip normalization by transform length, N.

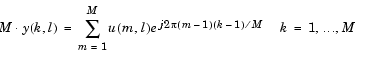
(7-4)

For information on block output characteristics and how to configure the block computation methods, see other sections of this reference page.

Sections of This Reference Page

Input and Output Characteristics

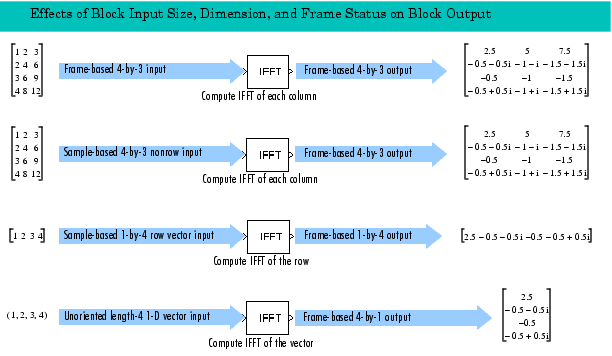
The following table describes all valid block input types, their corresponding outputs, and the dimension along which the block computes the IDFT.

Note For M-by-N and length-M inputs, M must be a power of two. To work with other input sizes, use the Zero Pad block to pad or truncate the length-M dimension to a power-of-two length. To get valid outputs, you must correctly set the Input is in bit-reversed order parameter to indicate the ordering of the block input. When the input is conjugate symmetric and you want to get a real-valued output, set the Input is conjugate symmetric parameter.

Valid Block Inputs
Must be complex-valued

M must be a power of two

In linear or bit-reversed order

Dimension Along Which Block Computes IDFT
Corresponding Block Output Characteristics
Output port rate = input port rate

Frame-based M-by-N matrix
Column
The following output characteristics apply to all valid block inputs:
Frame-based

Complex-valued unless you set the Input is conjugate symmetric parameter when your input is conjugate-symmetric, in which case the output is real-valued

Same dimension as input (for 1-D inputs, output is a length-M column)

Each column (each row for sample-based row inputs) contains the M-point IDFT of the corresponding input channel in linear order. If the parameter Skip normalization by transform length, N is set, rather than computing the IDFT, the block computes a scaled version of the IDFT given by Equation 7-4.

Sample-based M-by-N matrix,
Column

Sample-based 1-by-M row vector
Row

1-D length-M vector
Vector

Valid Block Inputs Must be complex-valued M must be a power of two In linear or bit-reversed order	Dimension Along Which Block Computes IDFT	Corresponding Block Output Characteristics Output port rate = input port rate
Frame-based M-by-N matrix	Column	The following output characteristics apply to all valid block inputs: Frame-based Complex-valued unless you set the Input is conjugate symmetric parameter when your input is conjugate-symmetric, in which case the output is real-valued Same dimension as input (for 1-D inputs, output is a length-M column) Each column (each row for sample-based row inputs) contains the M-point IDFT of the corresponding input channel in linear order. If the parameter Skip normalization by transform length, N is set, rather than computing the IDFT, the block computes a scaled version of the IDFT given by Equation 7-4.
Sample-based M-by-N matrix,	Column
Sample-based 1-by-M row vector	Row
1-D length-M vector	Vector

Click here in the MATLAB Help Browser to open a Simulink model based on the following diagram.

Conjugate Symmetric Input

When the block input is conjugate symmetric and you want real-valued outputs, set the Input is conjugate symmetric parameter, which also optimizes the block's computation method. A common source of conjugate symmetric data is the FFT block, which yields conjugate symmetric output when its input is real-valued.

Note If the IFFT block input is conjugate symmetric but you do not set the Input is conjugate symmetric parameter, you do not get a real-valued output. Instead, you get a complex-valued output with small imaginary parts. The block output is invalid if you set this parameter when the input is not conjugate symmetric.

Inputs in Bit-Reversed Order

When the block input is in bit-reversed order, you must set the parameter Input is in bit-reversed order to get a valid output. The block output is invalid if you set this parameter when the input is not in bit-reversed order. A common source of bit-reversed inputs is the FFT block, as illustrated in the FFT block example, Use of Outputs in Bit-Reversed Order.

For a definition of bit-reversed and linear order, see the FFT block reference page section, Description of Bit-Reversed Ordering.

Selecting the Twiddle Factor Computation Method

The FFT block and IFFT block both have a parameter, Twiddle factor computation. Setting this parameter in the IFFT block is very similar to setting it in the FFT block. For details, see the FFT block reference page section, Selecting the Twiddle Factor Computation Method.

Optimizing the Table of Trigonometric Values

The FFT block and IFFT block both have a parameter, Optimize table for. Setting this parameter in the IFFT block is very similar to setting it in the FFT block. For details, see the FFT block reference page section, Optimizing the Table of Trigonometric Values.

Algorithms Used for IFFT Computation

Depending on whether the block input is real- or complex-valued and conjugate symmetric, the block uses one or more of the following algorithms as summarized in the next table:

Radix-2 decimation-in-time (DIT) algorithm
Half-length algorithm
Double-signal algorithm

Input Complexity
Other Parameter Settings
Algorithms Used for FFT Computation

Complex
not applicable
Radix-2 DIT

Real

Radix-2 DIT

Real

Radix-2 DIT in conjunction with the half-length and double-signal algorithms when possible

Input Complexity	Other Parameter Settings	Algorithms Used for FFT Computation
Complex	not applicable	Radix-2 DIT
Real		Radix-2 DIT
Real		Radix-2 DIT in conjunction with the half-length and double-signal algorithms when possible

Example

For an example of how to optimize computations when using both the IFFT block and FFT block in the same model, see the FFT block reference page example, Use of Outputs in Bit-Reversed Order.

Dialog Box

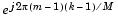Twiddle factor computation: Computation method of the term in Equation 7-3. In Table lookup mode, the block computes and stores the sine and cosine values before the simulation starts. In Trigonometric fcn mode, the block computes the sine and cosine values during the simulation.
Optimize table for: Optimization of the table of sine and cosine values for Speed or Memory. Active only when Twiddle factor computation is set to Table lookup.
Input is in bit-reversed order: Set when the input is in bit-reversed order, and clear when the input is in linear order. The block yields invalid outputs if you do not set this parameter correctly.
Input is conjugate symmetric: Set when the block input is conjugate symmetric and you want real-valued outputs. The block output is invalid if you set this parameter when the input is not conjugate symmetric.
Skip normalization by transform length, N: When set, rather than computing the IDFT, the block computes a scaled version of the IDFT given by Equation 7-4.

Supported Data Types

Double-precision floating point
Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

FFT
DSP Blockset

IDCT
DSP Blockset

Pad
DSP Blockset

Zero Pad
DSP Blockset

bitrevorder
Signal Processing Toolbox

fft
Signal Processing Toolbox

ifft
Signal Processing Toolbox

FFT	DSP Blockset
IDCT	DSP Blockset
Pad	DSP Blockset
Zero Pad	DSP Blockset
`bitrevorder`	Signal Processing Toolbox
`fft`	Signal Processing Toolbox
`ifft`	Signal Processing Toolbox

Also see Transforms for a list of all the blocks in the Transforms library.

IDWT Inherit Complexity