

| Using Simulink |   |
ライブラリ
詳細

Combinatorial Logicブロックは、プログラミング可能な論理配列(PLAs)、論理回路、決定表、その他のブール式をモデル化するための、標準の真理値表を実現します。このブロックはMemoryブロックと組み合わせて使用することにより、有限状態マシンやフリップフロップを実現することができます。
Truth table パラメータとして、すべての可能なブロック出力を定義する行列を指定します。行列の各行には、異なる入力要素の組み合わせが含まれています。入力のすべての組み合わせに対して、出力を指定する必要があります。列数は、ブロックの出力数です。
number of rows = 2 ^ (number of inputs)
Simulinkは、入力ベクトル要素から行のインデックスを計算することによって、行列の1つの行を出力します。Simulinkは、入力ベクトルのゼロ要素が0で、非ゼロ要素が1である2進数を作成することによってインデックスを計算し、結果に1を加算します。m 要素の入力ベクトル u の場合には、つぎのようになります。
row index = 1 + u(m)*20 + u(m-1)*21 + ... + u(1)*2m-1
2入力のAND関数の例
この例では、2つの入力要素がいずれも1のときに1を出力し、そうでないときに0を出力する2入力のAND関数を作成します。この関数を実現するには、Truth table パラメータ値を [0; 0; 0; 1] と指定します。Combinatorial Logicブロックに対して入力と出力を提供するモデルの一部は、つぎのようになります。
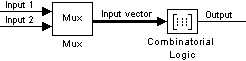
下の表は、各出力を生成する入力の組み合わせを示しています。"入力1" のラベルの付いた入力信号は、入力1のラベルの付いた表の列に対応します。同様に、"入力2" のラベルの付いた入力信号は、入力2の列に対応します。これらの値の組み合わせによって、表の出力列のどの行がブロック出力として渡されるかが決まります。
たとえば、入力ベクトルが [1 0] の場合、入力は第3行 (21*1 + 1) を参照します。したがって、出力値は0です。
| 行 |
入力1 |
入力2 |
出力 |
| 1 |
0 |
0 |
0 |
| 2 |
0 |
1 |
0 |
| 3 |
1 |
0 |
0 |
| 4 |
1 |
1 |
1 |
回路の例
このサンプル回路には3つの入力があります。加算される2つのビット(a と b)とキャリ-インビット(c)です。出力は、キャリ-アウトビット(c')と加算ビット(s)の2つです。以下に、真理値表とこの回路に対する入力値の組み合わせに関連した出力を示します。
| 入力 | 出力 | |||
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
1 |
この加算器をCombinatorial Logicブロックで実現するには、Truth table パラメータとして、c' と s の列で作られる8行2列の行列を入力します。
順序回路(すなわち、状態をもつ回路)もブロックの状態に対する入力を追加し、ブロックの出力をこの状態入力にフィードバックすることによって、Combinatorial Logicブロックで実現することができます。
サポートされているデータタイプ
Combinatorialブロックは、boolean または double タイプの実数信号を受け入れ、入力と同じタイプの出力を行います。真理表の要素は、boolean タイプでも、double タイプでも構いません。要素が double タイプの場合、"boolean" (0 または 1) 値だけでなく任意の値をとることができます。真理表要素のデータタイプが出力信号のデータタイプと異なる場合、Simulinkは、出力を計算する前に真理表を出力タイプに変換します。
パラメータとダイアログボックス
特性
| 直接フィードスルー |
あり |
| サンプル時間 |
接続されるブロックから継承 |
| スカラ拡張 |
不可 |
| ベクトル化 |
可、出力幅は Truth table パラメータの列数 |
| ゼロクロッシング |
なし |
 | Clock | Complex to Magnitude-Angle |  |