Signal Processing Toolbox

パラメトリック法

信号の長さが短い場合、パラメトリック法は、ノンパラメトリック法よりも高い解像度を提供します。二つの方法は、スペクトル推定へのアプローチが異なるもので、データから直接 PSD を推定する代わりに、データを白色雑音がある線形システムに入力した結果の出力として モデル 化するもので、結果として、その線形モデルのパラメータを推定するものです。

一般的に使用される線形システムモデルは、全極モデル で、z 平面の原点に、すべての零点をもつフィルタです。このようなフィルタへの白色雑音の出力は、自己回帰(AR)プロセスです。このために、これらの方法は、スペクトル推定の AR モデル と見なされます。

AR モデルは、データの PSD がある周波数で大きくなる、すなわち、"ピーク"を示すようにデータのスペクトルを適切に記述する傾向があります。多くの実際的なアプリケーションの中のデータは、"ピーク"を示すスペクトルをもつ傾向があり、AR モデルは、非常に有効になります。加えて、AR モデルは、比較的簡単に解くことのできる線形方程式を導きます。

Signal Processing Toolbox は、スペクトル推定に対して、つぎの AR 法を提供しています。

• Yule-Walker AR 法(自己相関法)
• Burg 法
• 共分散法
• 修正共分散法

すべての AR 法は、次式で得られる PSD を与えます。

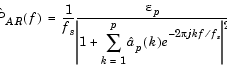
個々の AR 法は、AR パラメータ a_p(k) をわずかに異なる値で推定します。つぎの表は、種々の AR 法をまとめたものです。

	Burg	共分散	修正共分散	Yule-Walker
特性	データにウインドウを適用しません	データにウインドウを適用しません	データにウインドウを適用しません	データにウインドウを適用します
	Levinson 再帰法を満足すると言う制約の基で、AR 係数に対して、最小二乗的に、前置予測と後退予測誤差を最小にします。	最小二乗的に、前置予測誤差を最小にします。	最小二乗的に、前置と後退予測誤差を最小にします。	最小二乗的に、前置予測誤差を最小にします。 ("自己相関法"とも呼ばれます)
利点	短いデータに対して、高い解像度	短いデータに対して、Yule-Walker 法よりも良い解像度(より高い解像度)	短いデータに対して、高い解像度	長いデータ長に対して、他の方法と同様に機能
	常に安定モデルを作成	p または、複数の正弦波から構成されるデータから周波数を抽出することができます。	p または、複数の正弦波から構成されるデータから周波数を抽出することができます。	常に安定モデルを作成
			スペクトルライン分割は不可
欠点	ピークの位置が初期位相に非常に影響します	不安定なモデルを作成する可能性があります	不安定なモデルを作成する可能性があります	短いデータに対しては、質が比較的悪い
	雑音を含む正弦波に対してはスペクトルライン分割の可能性あり、または、次数が非常に高い場合に分割の可能性があります。	雑音の含まれた正弦波の推定にバイアスを含まれる可能性があります。	ピークの位置が初期位相に非常に影響します	雑音の含まれた正弦波の推定にバイアスを含まれる可能性があります。
	雑音の含まれた正弦波の推定にバイアスを含まれる可能性があります。		雑音の含まれた正弦波の推定にバイアスを含まれる可能性が少ない。
非正則性に対する条件		次数は、入力フレームサイズの半分に等しいか、以下です。	次数は、入力フレームサイズの2/3に等しいか、以下です。	バイアス推定のために、自己相関行列は、正定であることが保証され、そのために、特異にはなりません。

Yule-Walker AR 法

スペクトル推定の Yule-Walker AR 法 は、信号の自己相関関数のバイアス付き推定を作成し、前置予測誤差の二乗が最小になるように解き、AR パラメータを計算します。このことが、Yule-Walker 方程式で表わせます。

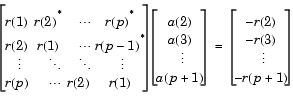
自己相関関数のバイアス付き推定の使用は、上の自己相関行列が正定である必要があります。そのため、行列が可逆で、解が存在することは保証されます。さらに、計算される AR パラメータは、安定な全極モデルに常になります。Yule-Walker 方程式は、Levinson アルゴリズムを使って、効率的に解くことができます。これは、自己相関行列の Toeplitz 構造を利用しています。

ツールボックス関数 pyulear は、Yule-Walker AR 法を実現します。

たとえば、Welch 法と Yule-Walker AR 法を使って、音声信号のスペクトルを求め、比較しましょう。

load mtlb
[P1,f] = pwelch(mtlb,hamming(256),128,1024,fs);
[P2,f] = pyulear(mtlb,14,1024,fs);
plot(f,10*log10(P1),':',f,10*log10(P2)); grid
ylabel('PSD Estimates (dB/Hz)');
xlabel('Frequency (Hz)');
legend('Welch','Yule-Walker AR')

実線は、Yule-Walker AR スペクトルで、これは、ピリオドグラムのものよりも、単純な全極モデルであるために、よりスムーズです。

Burg 法

AR スペクトル推定の Burg 法は、Levinson-Durbin 再帰法 (Marple [3], 7 章、Proakis [6], 12.3.3 節を参照) を満足して、前置後退予測誤差を最小にすることをベースにしています。他の AR 推定法と比べて、Burg 法は、自己相関関数を計算することを避け、代わりに、直接、反射係数を計算しています。

Burg 法の基本的な長所は、雑音レベルが低く、データ長が短い場合に、信号の中に存在する非常に近い周波数の正弦波を分解できることです。この場合、AR パワースペクトル密度推定は、真の値に非常に近いものになります。加えて、Burg 法は、安定な AR モデルを保証し、計算上も効率的です。

Burg 法の精度は、高次のモデル、データ長の長いもの、S/N 比が高いもの(これは、 スペクトルの中での ライン分割 、または、無数のピークをもつことになります)に対して、低くなります。Burg 法により計算されるスペクトル密度推定は、雑音を含んだ正弦波信号の初期位相に影響する周波数のシフトを受け入れます。この影響は、短いデータ列を解析する場合に、強調されます。

ツールボックス関数 pburg は、Burg 法を実現します。音声信号のスペクトルを、Burg 法と Yule-Walker AR 法を計算し、比較します。これらは、信号長が長い場合、非常に似た結果になります。

load mtlb
[P1,f] = pburg(mtlb(1:512),14,1024,fs);% 14 次のモデル
[P2,f] = pyulear(mtlb(1:512),14,1024,fs);% 14 次のモデル
plot(f,10*log10(P1),':',f,10*log10(P2)); grid
ylabel('Magnitude (dB)'); xlabel('Frequency (Hz)');
legend('Burg','Yule-Walker AR')

雑音を含んだ信号のスペクトルを、Burg 法と Welch 法を使って、計算し、比較します。

randn('state',0)
fs = 1000;           % サンプリング周波数
t = (0:fs)/fs;       % 0から1秒に時刻列を作成
A = [1 2];           % 正弦波の振幅
f = [150;140];       % 正弦波の周波数
xn = A*sin(2*pi*f*t) + 0.1*randn(size(t));
[P1,f] = pwelch(xn,hamming(256),128,1024,fs);
[P2,f] = pburg(xn,14,1024,fs);
plot(f,10*log10(P1),':',f,10*log10(P2)); grid
ylabel('PSD Estimates (dB/Hz)');
xlabel('Frequency (Hz)');
legend('Welch','Burg')

Burg 法に対するモデル次数を低くすると、正弦波の初期位相による周波数シフトがはっきりします。

共分散法と修正共分散法

AR スペクトル推定を行う共分散法は、前置予測誤差を最小にすることをベースにしています。修正共分散法は、前置/後退予測誤差を最小にすることをベースにしています。ツールボックスの関数 pcov と pmcov を使って、これらの処理を行うことができます。

共分散法と修正共分散法で作成した音声信号のスペクトルを比較しましょう。これらは、信号長が短い場合でさえ、ほぼ等しくなります。

load mtlb
[P1,f] = pcov(mtlb(1:64),14,1024,fs);% 14 次のモデル
[P2,f] = pmcov(mtlb(1:64),14,1024,fs);% 14 次のモデル
plot(f,10*log10(P1),':',f,10*log10(P2)); grid
ylabel('Magnitude (dB)'); xlabel('Frequency (Hz)');
legend('Covariance','Modified Covariance')

MUSIC と固有ベクトル解析法

関数 pmusic と peig は、2つの関係したスペクトル解析法を提供します。

• pmusic は、Schmidt により開発されたマルチプル信号分類(MUSIC)法を実現します。
• peig は、Johnson により開発された固有ベクトル(EV)法を実現します。

これらの手法のまとめについては、Marple [3] (373-378 ページ) を参照してください。

これらの手法は共に、自己相関行列の固有解析をベースにした周波数推定手法です。スペクトル解析のこの種のものは、情報を信号部分空間、または、雑音部分空間のいずれかに割り当てて、相関行列、または、データ行列の中に、情報を分類します。

固有解析の概要

白色雑音の中に含まれる数組の複素正弦波を考えましょう。このシステムを、信号の自己相関行列 (S) と雑音自己相関行列 (W) の和として、表わせる自己相関行列 R と書くことができます。

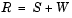
信号の自己相関行列と信号の部分空間、雑音の部分空間の固有ベクトルとの間には、密接な関係があります。S の固有ベクトル v は、信号ベクトルと同じ信号の部分空間を張ります。システムが、M 個の複素正弦波と次数が p の自己相関行列を含んでいる場合、v_M+1 から v_p+1 までの固有ベクトルは、自己相関行列の雑音の部分空間を張ることになります。

周波数推定子関数   周波数推定を作成するために、固有解析法は、信号の部分空間と雑音の部分空間で、ベクトルの関数を計算します。MUSIC 法と EV 法共に、入力信号の中で、正弦波の周波数の一つを無限大方向(分母をゼロ方向)に移動します。ディジタル理論を使って、結果の推定は、対象の周波数にシャープなピークを見ることができます。これは、ベクトルの中に∞値が存在していないことを意味しています。

MUSIC 推定は、つぎの式で与えられます。

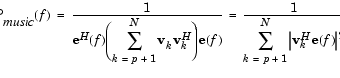
ここで、N は、固有ベクトルのサイズで、e(f) は、複素正弦波のベクトルです。

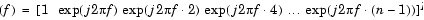
v は、入力信号の相関行列の固有値で、v_k は、k 番目の固有ベクトルです。H は、共役転置演算子です。和の中に使われている固有ベクトルは、最小の固有値に対応し、雑音空間を張ります(p は、信号部分空間のサイズです)。

表現 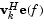は、フーリエ変換と等価です(ベクトル e(f) は、複素指数です)。FFT は、各 v_k に対して計算されるので、この型は、数値計算に利用可能です。それで、二乗した大きさは加算可能です。

EV 法は、相関行列の固有値で和に重み付けします。

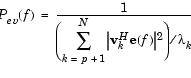
このツールボックスの中の関数 pmusic と peig は、信号の場合に、関数 svd (特異値分解) を使い、相関行列を解析するためには、関数 eig を使って、信号部分空間と雑音部分空間に固有ベクトルを割り当てます。svd が使われた場合、 pmusic と peig は、明示的に、相関行列を計算しませんが、特異値は固有値になります。

ノンパラメトリック法

参考文献