invfreqz (Signal Processing Toolbox)

周波数応答データから離散時間フィルタの同定

表示

[b,a] = invfreqz(h,w,nb,na)
[b,a] = invfreqz(h,w,nb,na,wt)
[b,a] = invfreqz(h,w,nb,na,wt,iter)
[b,a] = invfreqz(h,w,nb,na,wt,iter,tol)
[b,a] = invfreqz(h,w,nb,na,wt,iter,tol,'trace')
[b,a] = invfreqz(h,w,'complex',nb,na,...)

詳細

invfreqzは、freqzの逆の操作であり、与えられた複素周波数応答に対応する離散時間伝達関数を求めます。実験解析の見地から、invfreqzは、ゲインデータや位相データを伝達関数に変換するのに役立ちます。

[b,a] = invfreqz(h,w,nb,na) は、伝達関数の実数の分子係数ベクトルbおよび分母係数ベクトルaを出力します。

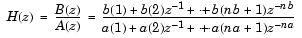
この複素周波数応答は、ベクトルwに設定した周波数点でベクトルhに与えられます。スカラnbおよびnaは、分子および分母多項式の希望の次数を設定します。

周波数は0との間でラジアン単位で設定し、hの長さはwの長さと同じでなければなりません。invfreqzは、-wでconj(h)を使って、実数フィルタに対して、適切な周波数領域の対称性を保証します。

[b,a] = invfreqz(h,w,nb,na,wt) は、周波数に対する近似誤差に重みを付けます。wtは、wと同じ長さの重み係数のベクトルです。

invfreqz(h,w,nb,na,wt,iter) および

invfreqz(h,w,nb,na,wt,iter,tol) は、数値的な反復法を使って、最適適合に対する探索を行い、結果の線形システムの安定性を保証する優れたアルゴリズムを実現します。iterパラメータは、解が収束するかあるいはiterに設定した反復回数に達するかのいずれかが先に起こったときに、invfreqzに反復を終了させます。invfreqzでは、(修正した)勾配ベクトルのノルムがtol未満となるときを収束と定義しています。tolは、オプションパラメータであり、デフォルトでは、0.01に設定されます。すべてが1の重みベクトルを得るには、つぎのステートメントを使用します。

invfreqz(h,w,nb,na,[],iter,tol)

invfreqz(h,w,nb,na,wt,iter,tol,'trace') は、反復の経過報告を文字で表示します。

invfreqz(h,w,'complex',nb,na,...) は、複素数のフィルタを作成します。この場合、対称性は要求されません。そして、周波数は、-との間でラジアンで設定されます。

例題

簡単な伝達関数を周波数応答データに変換し、ついでオリジナルのフィルタ係数に戻します。

a = [1 2 3 2 1 4]; b = [1 2 3 2 3];
[h,w] = freqz(b,a,64);
[bb,aa] = invfreqz(h,w,4,5)
bb =
    1.0000    2.0000    3.0000    2.0000    3.0000
aa =
    1.0000    2.0000    3.0000    2.0000    1.0000    4.0000

bbおよびaaは、bおよびaとそれぞれ等しくなることに注目してください。ただし、aaは単位円の外側に極をもつため、システムは不安定です。invfreqzの反復アルゴリズムを使って、システムに対する安定近似を求めます。

[bbb,aaa] = invfreqz(h,w,4,5,[],30)
bbb =
    0.2427    0.2788    0.0069    0.0971    0.1980
aaa =
    1.0000   -0.8944    0.6954    0.9997   -0.8933    0.6949

アルゴリズム

デフォルトでは、invfreqzは、式誤差法を使って、データから最良モデルを同定します。これは、

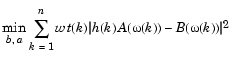
のbとaに関する連立1次方程式を作成し、MATLABの\演算子でそれを解くことにより求めます。ここで、A(w(k))およびB(w(k))は、それぞれ周波数w(k)での多項式aおよびbのフーリエ変換であり、nは周波数点数(hおよびwの長さ)です。このアルゴリズムは、Levi(参考文献[1])に基づいています。

より優れた("出力誤差")アルゴリズムでは、初期推定値として、最初のアルゴリズムの出力を使って、繰り返し探索に対して、減衰付きGauss-Newton法を使います(参考文献[2])。これは、実際の周波数応答点と希望の周波数応答点との間の2乗誤差の重み付き和を最小化する直接的な問題を解きます。

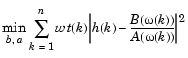
参考

freqs
アナログフィルタの周波数応答

freqz
ディジタルフィルタの周波数応答

invfreqs
周波数データからの連続系(アナログ)フィルタの同定

prony
時間領域IIRフィルタ設計に対するProny法

`freqs`	アナログフィルタの周波数応答
`freqz`	ディジタルフィルタの周波数応答
`invfreqs`	周波数データからの連続系(アナログ)フィルタの同定
`prony`	時間領域IIRフィルタ設計に対するProny法

参考文献

[1] Levi, E.C., "Complex-Curve Fitting," IRE Trans. on Automatic Control, Vol. AC-4 (1959), pp. 37-44.

[2] Dennis, J.E., Jr., and R.B. Schnabel, Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Prentice-Hall, 1983.

invfreqs is2rc