

| Signal Processing Toolbox |   |
遷移帯域付き複数帯域FIRフィルタ設計
関数firlsおよび関数remezは、関数fir1や関数fir2よりも希望する理想フィルタを設定する、より一般的な手段を提供します。これらの関数は、Hilbert変換器、微分器、およびその他の奇数対称係数をもつフィルタ(III型およびIV型の線形位相フィルタ)を設計します。これらは、また、誤差が最小とはならない遷移帯域すなわち、あまり気にしない領域を含むようにし、帯域依存の最小化の重み付けを行います。
関数 firlsは、希望の周波数応答と実際の周波数応答との間の誤差の二乗和を最小にするという点でfir1およびfir2を拡張したものです。
関数 remez は、Parks-McClellanアルゴリズムを実現するものです。これは、Remez交換アルゴリズムとChebyshev近似理論を用いて、希望する周波数応答と実際の周波数応答が最適になるようにフィルタを設計します。このフィルタは、希望する周波数応答と実際の周波数応答との間の最大誤差を最小にする点で最適であり、場合によっては、ミニマックスフィルタとも呼ばれます。この方法で設計されたフィルタは、その周波数応答において等リップルを示すため、等リップルフィルタとしても知られています。Parks-McClellan FIRフィルタ設計アルゴリズムは、おそらく、最も一般的で広く使用されているFIRフィルタ設計法と思われます。
firlsおよびremez の構文は、基本的には同じであり、唯一の違いは、最小化の規範についてです。つぎの例題では、firlsとremez で設計されたフィルタが、これらの異なる規範をどのように反映するかについて示します。
基本構成
firlsおよびremezのデフォルトの演算モードでは、希望するフィルタの次数が奇数か偶数かに応じて、それぞれI型またはII型の線形位相フィルタを設計します。たとえば、0〜0.4 Hzの近似振幅が1で、0.5〜1.0 Hzの近似振幅が0であるローパスフィルタは、つぎのようになります。
n = 20; % フィルタの次数 f = [0 .4 .5 1]; % 周波数帯域エッジ a = [1 1 0 0]; % 希望の振幅 b = remez(n,f,a);
0.4〜0.5 Hzでは、 remezは誤差の最小化を行いません。すなわち、この帯域が遷移帯域すなわち配慮されない領域です。遷移帯域では、遷移部分の割合を小さくして、"気にしない"帯域で誤差をより最小にします。このようにして、この種のフィルタは、ウィンドウによるFIR設計と同様の固有のトレードオフをもちます。
最小二乗フィルタ設計と等リップルフィルタ設計とを比較するには、つぎのようにしてfirlsを用いて同様のフィルタを作成し、
bb = firls(n,f,a);
[H,w]=freqz(b); [HH,w]=freqz(bb); plot(w/pi,abs(H),w/pi,abs(HH),'--'), grid
remezで設計されたフィルタは、等リップルの挙動を示していることがわかります。また、firlsフィルタは、通過帯域と遮断帯域のほぼ全体にわたり良好な応答を示していますが、帯域エッジ(f = 0.4およびf = 0.5)では、応答はremezフィルタ以上に理想から掛け離れています。これは、remezフィルタの最大誤差が通過帯域および遮断帯域上でより小さくなることを示しており、実際に、remezフィルタが、この帯域エッジ構成とフィルタ長に対して可能な限り最小の長さになっています。
周波数帯域を短い周波数間隔での線として考えます。remezおよびfirlsは、この方式を用いて、任意の遷移帯域をもつ希望の区分的線形関数を表現します。firlsおよびremezは、ローパスフィルタ、ハイパスフィルタ、バンドパスフィルタ、およびバンドストップフィルタを設計します。つぎに示すのは、バンドパスフィルタの例です。
f = [0 0.3 0.4 0.7 0.8 1]; % 設定する周波数点 a = [0 0 1 1 0 0]; % バンドパスフィルタの振幅
専門的に言うと、これらのfおよびaベクトルは、つぎの5つの帯域を定義します。
つぎに、ハイパスフィルタとバンドストップフィルタの例を示します。
f = [0 0.7 0.8 1]; % 設定する周波数点 a = [0 0 1 1]; % ハイパスフィルタの振幅 f = [0 0.3 0.4 0.5 0.8 1]; % 設定する周波数点 a = [1 1 0 0 1 1]; % バンドストップフィルタの振幅
f = [0 0.1 0.15 0.25 0.3 0.4 0.45 0.55 0.6 0.7 0.75 0.85 0.9 1]; a = [1 1 0 0 1 1 0 0 1 1 0 0 1 1];
他に可能なものとしては、通過帯域と遮断帯域とを結ぶ線を遷移領域とするフィルタがあります。これは、広範な遷移領域で、大きな差のあるランナウェイゲイン応答を制御するのに役立ちます。
f = [0 0.4 0.42 0.48 0.5 1]; a = [1 1 0.8 0.2 0 0]; % 通過帯域、線形遷移、遮断帯域
重みベクトル
firlsとremezでは共に、ある周波数帯域での誤差の最小化を他の周波数帯域での誤差の最小化と比べて重みを付けて、強調することができます。これを行うには、周波数ベクトルと振幅ベクトルの後に重みベクトルを設定します。つぎに示すものは、遮断帯域内に通過帯域の1/10のリップルをもつローパス等リップルフィルタの例です。
n = 20; % フィルタの次数 f = [0 0.4 0.5 1]; % 設定する周波数点 a = [1 1 0 0]; % 希望の振幅 w = [1 10]; % 重みベクトル b = remez(n,f,a,w);
正しく設定される重みベクトルは、常にベクトルfおよびベクトルaの長さの1/2になります。つまり、1つの帯域当たりの重みは、厳密に1つでなければなりません。
非対称フィルタ/Hilbert変換
入力引数の最後に 'h' 、つまりHilbertオプションを付けて呼び出すと、 remez および firls は、奇数対称性をもつFIRフィルタ、すなわちIII型(偶数次数の場合)またはIV型(奇数次数の場合)の線形位相フィルタを設計します。理想的なHilbert変換器は、周波数範囲全体にわたり、この非対称性特性と1の振幅をもちます。つぎの近似Hilbert変換器を試してみてください。
b = remez(21,[0.05 1],[1 1],'h'); % ハイパスHilbert bb = remez(20,[0.05 0.95],[1 1],'h'); % バンドパスHilbert
これらのフィルタに適用することにより、信号xの遅延されたHilbert変換を求めることができます。
fs = 1000; % サンプリング周波数 t = (0:1/fs:2)'; % 2秒の時間ベクトル x = sin(2*pi*300*t); % 300 Hzの正弦波サンプル信号 xh = filter(bb,1,x); % xのHilbert変換
xに対応する解析的信号は、xと同じ実数部をもち、xのHilbert変換を虚数部とする複素数になります。このFIR手法(関数hilbertの代用)では、解析的信号を作成するためにフィルタ次数の1/2だけxを遅れさせる必要があります。
xd = [zeros(10,1); x(1:length(x)-10)]; % 10サンプルの遅れ
xa = xd + j*xh; % 解析的信号
この手法は、非整数の遅れを必要とする奇数次数のフィルタには直接働きません。この場合には、"特殊変換"で説明するように、関数 hilbert を使って、解析的信号を推定します。あるいは、関数 resampleを用いて、サンプルの非整数の数だけ信号を遅らせます。
微分器
時間領域内の信号の微分は、信号のフーリエ変換に虚数のランプ関数を乗算したものに相当します。すなわち、信号を微分するには、その信号を応答H(w) = jwをもつフィルタに通すことになります。つぎのように、'd'、または'differentiator'オプションを付けたremez またはfirls を用いて理想的な微分器(遅れを伴う)に近似させます。
b = remez(21,[0 1],[0 pi*fs],'d');
正確な導関数を得るには、 pi*fs ラジアン/秒でスケーリングします。ここで、fsはヘルツ単位のサンプリング周波数です。III型フィルタの場合には、微分帯域はNyquist周波数より低く、振幅ベクトルは、その変化を反映して正確なスロープを確保していなければなりません。
bb = remez(20,[0 0.9],[0 0.9*pi*fs],'d');
remezは、'd'モードでは非ゼロ振幅帯域において、1/ だけ誤差に重みを付けて、最大相対誤差を最小化します。
だけ誤差に重みを付けて、最大相対誤差を最小化します。firlsは、'd'モードでは非ゼロ振幅帯域において、(1/ )2だけ誤差に重みを付けます。
)2だけ誤差に重みを付けます。
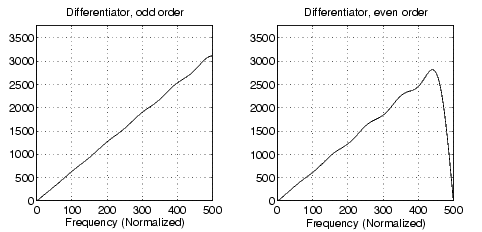
以上示した微分器のゲイン応答プロットは、つぎのようになります。
 | ウィンドウ法 | 制約付き最小二乗FIRフィルタの設計 |  |