

| Signal Processing Toolbox |   |
線形システムモデル
Signal Processing Toolboxには、線形時不変システムを表現するためのいくつかのモデルが用意されています。種々のモデルにより、ユーザのアプリケーションに最も適した表現方式を選択することや、数値的に安定な範囲内で自由に他のほとんどのモデル表現との変換を行うことができます。本節では、サポートされている線形システムモデルを概説し、MATLABにおけるこれらのモデルの使用法を説明します。
離散時間システムモデル
離散時間システムモデルは、ディジタルフィルタの代表的なものです。MATLABは、つぎに示すいくつかの離散時間システムモデルをサポートしています。
伝達関数型
伝達関数は、ディジタルフィルタの基本的なz領域表現であり、フィルタを2つの多項式の比として表現します。この表現は、このツールボックスの重要な離散時間モデルです。ディジタルフィルタの差分方程式のz変換に対する伝達関数モデル表現は、つぎのようになります。
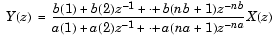
ここで、定数b(i)とa(i)はフィルタ係数であり、フィルタの次数はnaとnbの最大値となります。MATLABでは、これらの係数を2つのベクトル(通常、行ベクトル)に格納します。このとき、一方の行ベクトルには分子、もう一方には分母を、それぞれ格納します。伝達関数型の詳細については、1-16ページの"フィルタと伝達関数"を参照してください。
零点-極-利得
伝達関数の因子分解型、または、"零点-極-利得"型は、つぎのように表現されます。
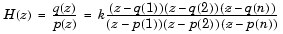
通常、MATLABでは多項式の係数を行ベクトルに、多項式の根を列ベクトルに、それぞれ格納します。従って、零点-極-利得型では、伝達関数の分子と分母の零点および極の位置は、列ベクトルで表します。因数分解した伝達関数のゲインkは、MATLABのスカラとして表します。
関数polyおよびrootsは、多項式表現と零点-極-利得表現間を変換します。たとえば、つぎの簡単なIIRフィルタを考えます。
b = [2 3 4]; a = [1 3 3 1];
q = roots(b)
q =
-0.7500 + 1.1990i
-0.7500 - 1.1990i
p = roots(a)
p =
-1.0000
-1.0000 + 0.0000i
-1.0000 - 0.0000i
k = b(1)/a(1)
k =
2
bb = k*poly(q)
bb =
2.0000 3.0000 4.0000
aa = poly(p)
aa =
1.0000 3.0000 3.0000 1.0000
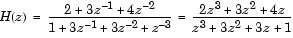
b = [2 3 4]の場合、関数rootsは、zに対して0である零点を省略します。入力伝達関数で、零点よりも極のほうが多く入力された場合、0になる零点を省略します。また、逆に極よりも零点のほうが多く入力された場合、0になる極を省略します。ほとんどの場合、これは問題とはなりませんが、仮に、問題が生じた場合、回避するには、たとえば、b = [b 0]のように関数rootsを使うときに0を付加して、ベクトルを同じ長さにしてください。
状態空間(State space)型
ディジタルフィルタ、または、差分方程式のシステムは、常に、1次差分方程式の集合として表現することができます。行列または状態空間(State space)型では、その方程式を、つぎのように記述することができます。
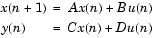
ここで、uは入力、xは状態ベクトル、yは出力です。単一チャンネルシステムの場合、Aはmをフィルタの次数とするm行m列の行列であり、Bは列ベクトル、Cは行ベクトル、そして、Dはスカラです。状態空間(State space)表記法は、入力uと出力yがベクトルとなり、B、C、およびDが行列となる多チャンネルシステムの場合に特に便利です。
状態空間(State space)表現は、MATLAB環境に容易に拡張されます。MATLABでは、A、B、C、およびDは、長方形配列であり、独立な変数として扱われます。
状態空間(State space)方程式をz変換して、それらを組み合せると、状態空間型と伝達関数型は等価であることがわかります。
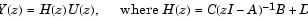
線形システムの状態空間(State space)表現を熟知していなくても心配する必要はありません。いくつかのフィルタ設計アルゴリズムでは状態空間型を内部的に使用していますが、それらをうまく使用するのに状態空間概念に関する知識は必要ありません。ただし、ユーザの使うアプリケーションが、状態空間型をベースに信号処理を拡張している場合、状態空間型を広く使っているライブラリのControl System Toolboxを参考にしてください。
部分分数展開(留数)型
伝達関数は、また、次式によって与えられる部分分数展開、または留数型表現があります。
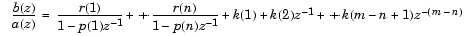
ただし、H(z)には重複極がないものとします。ここで、nは、有理伝達関数b(z)/a(z)の分母多項式の次数です。rが重複度srの極の場合、H(z)はつぎの形式の項をもちます。
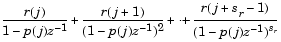
Signal Processing Toolboxの関数residuezは、伝達関数型と部分分数展開型とをお互いに変換します。residuezの末尾の"z"は、z領域、すなわち離散領域を表しています。residuezは、極を列ベクトルpに、その極に対応する留数を列ベクトルrに、また、オリジナルの伝達関数のすべての仮分数を行ベクトルkにそれぞれ出力します。residuezは、2つの極の差分の大きさがいずれか一方の極の大きさの0.1パーセントより小さければ、それら2つの極は同一であると判定します。
部分分数展開は、信号処理において伝達関数の逆z変換を求める方法の1つとして生まれたものです。たとえば、
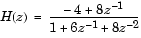
b = [--4 8];
a = [1 6 8];
[r,p,k] = residuez(b,a)
r =
-12
8
p =
-4
-2
k =
[]
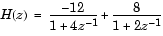
H(z)の逆z変換を求めるには、H(z)を和の型で表している2つの要素の逆z変換の和で求まります。これは、因果的なインパルス応答を与えます。
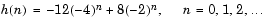
imp = [1 0 0 0 0];
resptf = filter(b,a,imp)
resptf =
-4 32 -160 704 -2944
respres = filter(r(1),[1 -p(1)],imp) + filter(r(2),[1 -p(2)],imp)
respres =
-4 32 -160 704 -2944
2次型(SOS)
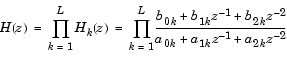
ここで、Lはシステムを表す2次型の数です。MATLABでは、離散時間システムに対する2次型をL行6列の配列sosとして表現します。sosの各行は1つの2次型を含み、この場合、行要素は2次型を表す3つの分子と3つの分母の係数です。
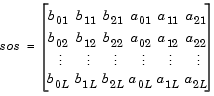
2次型でフィルタを表現する方法は無数にあります。極と零点を慎重に組み合わせたり、カスケード内の順序を変更したり、また、スケーリングすることにより、量子化ノイズゲインを抑え、いくつかの固定小数点フィルタ実現の際のオーバフローを防止することができます。後述する"線形システム変換"で説明する関数zp2sosおよびss2sosは、極-零点の組み合わせ、スケーリング、および各2次型の順序付けを行います。
ラティス構造
多項式の係数a(n), n = 1,2,…,N+1によって表されるN次の全極、または全零点の離散フィルタには、対応するN個のラティス構造係数k(n), n = 1,2,…,Nがあります。パラメータk(n) は、フィルタの反射係数とも呼ばれます。これらの反射係数を与えると、つぎのように離散フィルタを実現することができます。
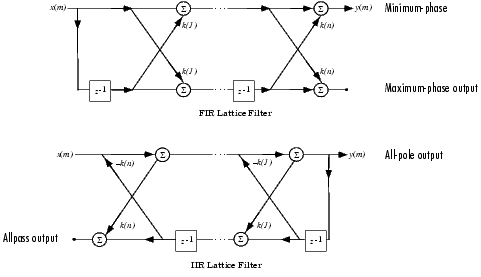
多項式の係数aとbによって表される一般的な極-零点IIRフィルタには、分母aに対するラティス係数k(n)と分子bに対するラダー係数v(n)の両方があります。ラティス/ラダー型フィルタは、つぎのように実現することができます。
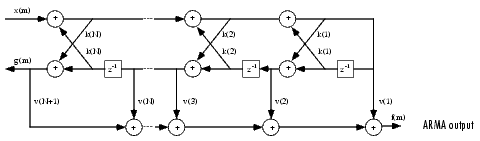
ツールボックス関数 tf2latc は、多項式型の FIR、または、IIR フィルタを入力とし、対応する反射係数を出力します。多項式の型での例題の FIR フィルタは、つぎの型をしているとします。
b = [1.0000 0.6149 0.9899 0.0000 0.0031 -0.0082];
このフィルタのラティス (反射係数) 表現は、つぎのようになります。
k = tf2latc(b)
k =
0.3090
0.9801
0.0031
0.0081
-0.0082
IIR フィルタに対して、反射係数の大きさを使って、安定チェックが簡単にできます。多項式に対応する反射係数のすべてが、1より小さい場合、多項式の根はすべて単位円の内側に位置します。たとえば、上で記述した分子多項式 b とつぎの分母多項式をもつ IIR フィルタを考えましょう。
a = [1 1/2 1/3];
[k,v] = tf2latc(b,a)
k =
0.3750
0.3333
0
0
0
v =
0.6252
0.1212
0.9879
-0.0009
0.0072
-0.0082
k に含まれるすべての反射係数の絶対値が1より小さいので、フィルタは安定です。
関数latc2tfは、そのラティス(反射)係数からフィルタの多項式係数を計算します。反射係数ベクトルk(上記の)を与えると、対応する多項式型は、つぎのようになります。
a = latc2tf(k)
a =
1.0000 0.6149 0.9899 -0.0000 0.0031 -0.0082
このラティス係数またはラティス/ラダー係数は、関数latcfiltを用いて、フィルタを実現するのに使用することができます。
コンボリューション行列型
信号処理において、2つのベクトル、または、行列のコンボリューションを行うことは、一方の入力オペランドを他方の入力オペランドでフィルタ処理することと同じです。この関係を使って、ディジタルフィルタの表現をコンボリューション行列とすることができます。
任意のベクトルを与えると、ツールボックスの関数convmtxは、もう一方のベクトルとの内積を計算し、2つのベクトルのコンボリューションと等しくなる行列を生成します。生成された行列は、適切な長さの任意のベクトルに適用することができるディジタルフィルタを表します。すなわち、オペランド間の次元は内積の計算が可能なようになります。
ディジタルフィルタの分子の係数を表すベクトルbとのコンボリューション行列は、つぎのようになります。
b = [1 2 3]; x = randn(3,1);
C = convmtx(b',3)
C =
1 0 0
2 1 0
3 2 1
0 3 2
0 0 3
bとxのコンボリューションを行うには、つぎの2つの方法があります。
y1 = C*x;
y2 = conv(b,x);
 | 零点-極解析 | 連続時間システムモデル |  |