Signal Processing Toolbox

フィルタの実現と解析

本節では、MATLAB の関数 filter や他の Signal Processing Toolboxの関数を用いて、離散信号をフィルタ処理する方法を説明します。また、ツールボックスの関数を用いて、インパルス応答、ゲイン応答、位相応答、群遅延、零点-極位置などのフィルタ特性を解析する方法も検討します。

コンボリューションとフィルタ処理

フィルタ処理の数学的基礎は、コンボリューションです。MATLABの関数convは、標準の1次元コンボリューション、つまり、あるベクトルと別のベクトルの乗算を行います。

conv([1 1 1],[1 1 1])
ans =
     1     2     3     2     1

注意   2次元信号処理の場合、関数conv2を用いて、長方形行列に対するコンボリューションを行います。

ディジタルフィルタの出力y(n)は、そのインパルス応答h(n)と、入力x(n)とのコンボリューションによって、表わされます。

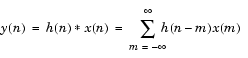
ディジタルフィルタのインパルス応答h(n)が有限長であり、かつ、入力x(n) も有限長の場合、convを用いて、フィルタ演算を実現することができます。x(n) をベクトルxに、h(n)をベクトルhに、それぞれ格納し、2つのベクトルのコンボリューションを行うには、つぎのようにします。

x = randn(5,1);   % 長さ5のランダムベクトル
h = [1 1 1 1]/4;  % 長さ4の平均化を行なうフィルタ
y = conv(h,x);

データの扱い

フィルタと伝達関数