| 計算の信頼性 | |
伝達関数
項を展開した多項式によって表された伝達関数モデルは、本質的に、条件数の悪いLTIシステムの表現となる傾向があります。10次を越える次数のシステム、あるいは非常に大きいか非常に小さい多項式係数をもつシステムの場合、roots、conv、bode、stepなどの関数、または、ss、zpkなどの変換関数では問題が生じる可能性があります。
大きな問題の1つは、多項式の根のその係数に対する敏感な感度です。この例題は、それを示すためにWilkinson[6]から採用しました。つぎの伝達関数について考えます。
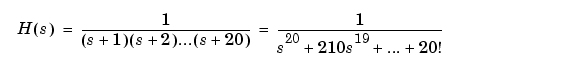
これに対応する
のコンパニオン実現の行列
は、つぎのとおりです。
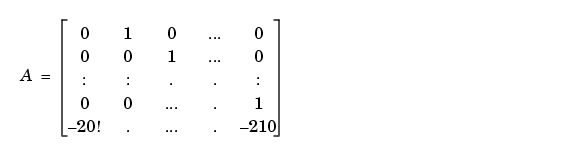
(-1,-2,...,-20 での)システムの極は見かけは良好ですが、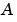
の要素における、より大きな範囲の数値1から
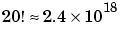に直面します。しかし、問題はここで終わるわけではありません。伝達関数(つまり、
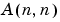)における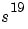
の係数が210から
(
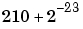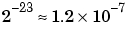)まで摂動の影響を受けたと仮定します。その場合、VAX(IEEE算術は、 
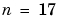の場合にのみ十分な仮数をもっています)上で計算すると、摂動の影響を受けた伝達関数(等価的に
の固有値)は、つぎのようになります。
eig(A)' ans = Columns 1 through 7 -19.9998 -19.0019 -17.9916 -17.0217 -15.9594 -15.0516 -13.9504 Columns 8 through 14 -13.0369 -11.9805 -11.0081 -9.9976 -9.0005 -7.9999 -7.0000 Columns 15 through 20 -6.0000 -5.0000 -4.0000 -3.0000 -2.0000 -1.0000
ここでの問題は、丸めではありません。むしろ、原点が十分に分離されても、高次の多項式は、本質的に非常に高い感度をもっています。この場合、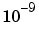
のオーダの相対的摂動は、根によっては
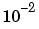のオーダの摂動を引き起こしています。しかし、根の中には、ほとんど変化していないものもあります。これは一般的な事実です。異なる根は、異なる摂動に対して異なる感度をもっています。従って、不正確な既知の係数をもつ、特に高次の多項式にとって、計算した根がまったく無意味となる場合もあります。
多項式のすべての根(等価的に伝達関数の極または可制御正準型か、可観測正準型行列の固有値)を見つけることは、多くの場合、本質的に微妙な問題です。困難な縮退数値問題など、この問題の明確かつ詳細な取り扱いについては、[6]を参照してください。
従って、できるだけ多項式の因数分解した形式で作業を行うほうが望ましいと言えます。たとえば、上で定義した伝達関数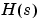
の状態空間モデルを計算するには、つぎのように
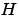の分母を展開し、伝達関数モデルを状態空間モデルに変換し、状態空間データを抽出することができます。
H1 = tf(1,poly(1:20)) H1ss = ss(H1) [a1,b1,c1] = ssdata(H1)
ただし、分母は、因数分解した形のまま保持し、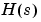
の零点-極-ゲイン表現で計算を実行しなければなりません。
H2 = zpk([],1:20,1) H2ss = ss(H2) [a2,b2,c2] = ssdata(H2)
実際、結果として得られる状態行列a2 は、条件数が改善されています。
[cond(a1) cond(a2)] ans = 2.7681e+03 8.8753e+01
また、零点-極-ゲインから状態空間型への変換では、極の精度は失われません。
format long e
[sort(eig(a1)) sort(eig(a2))]
ans =
9.999999999998792e-01 1.000000000000000e+00
2.000000000001984e+00 2.000000000000000e+00
3.000000000475623e+00 3.000000000000000e+00
3.999999981263996e+00 4.000000000000000e+00
5.000000270433721e+00 5.000000000000000e+00
5.999998194359617e+00 6.000000000000000e+00
7.000004542844700e+00 7.000000000000000e+00
8.000013753274901e+00 8.000000000000000e+00
8.999848908317270e+00 9.000000000000000e+00
1.000059459550623e+01 1.000000000000000e+01
1.099854678336595e+01 1.100000000000000e+01
1.200255822210095e+01 1.200000000000000e+01
1.299647702454549e+01 1.300000000000000e+01
1.400406940833612e+01 1.400000000000000e+01
1.499604787386921e+01 1.500000000000000e+01
1.600304396718421e+01 1.600000000000000e+01
1.699828695210055e+01 1.700000000000000e+01
1.800062935148728e+01 1.800000000000000e+01
1.899986934359322e+01 1.900000000000000e+01
2.000001082693916e+01 2.000000000000000e+01
ssを用いて状態空間形式で実現した場合、伝達関数モデルには別の問題が伴います。固有値の分離が適切であっても、条件数の悪い固有ベクトル行列を生じる場合があります。たとえば、つぎの正規行列についてを考えてみます。
A = [5 4 1 1
4 5 1 1
1 1 4 2
1 1 2 4]
[v,d] = eig(A)
v =
0.7071 -0.0000 -0.3162 0.6325
-0.7071 0.0000 -0.3162 0.6325
0.0000 0.7071 0.6325 0.3162
-0.0000 -0.7071 0.6325 0.3162
d =
1.0000 0 0 0
0 2.0000 0 0
0 0 5.0000 0
0 0 0 10.0000
固有ベクトル行列の(逆行列に関しての)条件数は、つぎのようになります。
cond(v)
ans =
1.000
上記のA行列をもつ状態空間モデルを伝達関数形式に変換し、再び状態空間形式に戻します。
b = [1 ; 1 ; 0 ; -1]; c = [0 0 2 1]; H = tf(ss(A,b,c,0)); % 伝達関数 [Ac,bc,cc] = ssdata(H) % 状態空間形式に戻す
Ac =
18.0000 -6.0625 2.8125 -1.5625
16.0000 0 0 0
0 4.0000 0 0
0 0 1.0000 0
Ac は、標準のコンパニオン行列ではなく、ss変換の一部として、すでに平衡化されていることに注意してください(詳細については、 ssbalを参照してください)。
[vc,dc] = eig(Ac)
vc =
-0.5017 0.2353 0.0510 0.0109
-0.8026 0.7531 0.4077 0.1741
-0.3211 0.6025 0.8154 0.6963
-0.0321 0.1205 0.4077 0.6963
dc =
10.0000 0 0 0
0 5.0000 0 0
0 0 2.0000 0
0 0 0 1.0000
cond(vc)
ans =
34.5825
上に示した現象は、異常ではありません。(Acのように)コンパニオン形式または可制御正準型か可観測正準型の行列は、概して(A のように)一般の状態空間形式の行列より悪い条件数の固有システムをもっています。これは、それらの固有値や固有ベクトルが摂動の影響をより受け易いことを意味しています。また、高次システムでは問題は一般にはるかに悪化します。従って、高次の伝達関数モデルを取り扱う場合、状態空間との間で、それらの変換、逆変換を繰り返すことは数値的に危険を伴います。
要するに、伝達関数モデルを取り扱う際(従って、多項式を伴う計算を行う際)に留意すべき主な数値問題は、つぎのとおりです。
ssで生成した平衡化のとれたコンパニオン形式は、標準のコンパニオン形式より優れていますが、特に高次システムでは、条件数の悪い固有問題を生じる場合が多くあります。上記の条件は、明確な極をもつシステムに対しても適用されますが、特に、極が複数の場合にあてはまります。
| | 状態空間 | 零点−極−ゲインモデル | |