モデルの作成と取り扱い

伝達関数

この節は、連続時間SISOとMIMO伝達関数モデルの設定の仕方を説明します。離散時間伝達関数モデルの設定は、連続時間伝達関数を拡張したものです("離散時間モデル"を参照)。この節で、ゲインのみからなる伝達関数の設定法についても記述します。

SISO伝達関数モデル

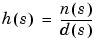
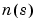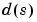は、その分子および分母で特徴付けられた、いずれもLaplace変数sの多項式です。

SISO伝達関数を設定する2つの方法があります。

• tfコマンドを使う。
• Laplace変数sを使って、有理数表現を行なう。

SISO伝達関数モデルを、tfを使って設定しましょう。

h = tf(num,den)

ここで、numとden は、多項式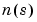と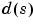の係数をsのベキ乗の次数の高いほうから並べた結果の変数 hは、分子データと分母データを含むTFオブジェクトです。

たとえば、つぎのようにタイプすることで、伝達関数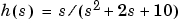を作成できます。

h = tf([1 0],[1 2 10])

MATLABは、つぎの出力を得ます。

Transfer function:
       s
--------------
s^2 + 2 s + 10

MATLABは、TFオブジェクトに使用するカスタマイズした表示に注意してください。

Laplace変数sの有理数表現として伝達関数をつぎのように設定することができます。

1. 変数を特別なTFモデルとして定義します。

   s = tf('s');
   

2. 伝達関数をsの有理数表現として入力します。

たとえば、sを1と言う文字列としてtfで設定すると、

H = s/(s^2 + 2*s +10);

は、つぎの伝達関数と同じものを作成します。

h = tf([1 0],[1 2 10]); 

注意    変数sをTFモデルとして定義する必要があります。ZPKに変数sを変換しない限り、sの有理数表現を使って作成した一連のモデルはすべて、TFオブジェクトとして設定されます。詳細は、2-42ページの"モデルの変換"を参照してください。

MIMO伝達関数モデル

MIMO伝達関数は、基本的なSISO伝達関数の2次元配列です。MIMO伝達関数モデルを設定するためにいくつかの方法があります。

• SISO伝達関数モデルの連結
• tfをセル配列引数と共に使用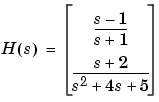

つぎの有理伝達行列を考えます。

ここで、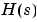をSISOを連結したものとして設定します。たとえば、

h11 = tf([1 -1],[1 1]);
h21 = tf([1 2],[1 4 5]);

または、つぎのものも等価です。

s = tf('s')
h11 = (s-1)/(s+1);
h21 = (s+2)/(s^2+4*s+5); 

を使って、連結してを作成します。

H = [h11; h21]

この構文は、標準的な行列の連結に類似したもので、複数の入力と出力をもつMIMOシステムに対して、より簡単で、より理解し易いものです。LTIシステムの連結演算に関する詳細は、"モデルの内部相互結合関数"を参照してください。

また、tfを使って、MIMO伝達関数を定義するため、分子多項式と分母多項式をそれぞれ表わす2つの配列(NとD)が必要になります。セル配列に関する詳細は、Using MATLAB の"構造体とセル配列"を参照してください。

たとえば、有理伝達行列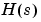に対して、2つのセル配列NとDを、つぎの多項式で表わされた行ベクトルとします。

つぎのようにタイプして、このMIMO伝達行列を設定します。

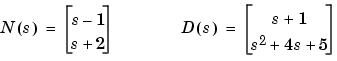
N = {[1 -1];[1 2]}; % 多項式配列N(s)
D = {[1 1];[1 4 5]}; % 多項式配列D(s)
H = tf(N,D)

MATLABは、つぎの出力を行います。

Transfer function from input to output...
      s - 1
 #1:  -----
      s + 1
 
          s + 2
 #2:  -------------
      s^2 + 4 s + 5

NとDは共にHと同じ次元であることに注意してください。一般的なMIMO伝達行列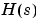に対して、セル配列のN{i,j}およびD{i,j}は、伝達行列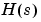の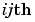 番目の要素、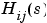の分子と分母の行ベクトル表現でなければなりません。

ゲインのみの場合

単純なゲインまたはゲイン行列をTFオブジェクトとして指定するには、引数を一つのみ使って、tfコマンドを使います。たとえば、

G = tf([1 0;2 1])

は、ゲイン行列

を作成し、一方、

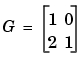
E = tf

は、空の伝達関数を出力します。

LTIモデルの作成

零点/極/ゲインモデル