モデルの作成と取り扱い

遅れを含むシステムの離散化

c2dを使って、むだ時間を含むSISOまたはMIMO連続時間モデルを離散化することができます。Tsを離散化に使うサンプリング周期としましょう。

• 連続時間モデルの中でtau秒の遅れは、離散化されたモデルの中で、k個のサンプリング周期の遅れとなります。ここで、k = fix(tau/Ts)です。
• 離散化によるサンプル周期より小さい部分tau - k*Tsは、離散化モデルの中の係数に含ませます(この方法は、ゼロ次ホールド、一次ホールドのみ)。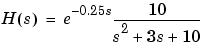

たとえば、つぎの伝達関数

を離散化するため、入力に10Hzのサンプリングレートでゼロ次ホールドを適用します。

h = tf(10,[1 3 10],'inputdelay',0.25);
hd = c2d(h,0.1)

つぎの離散時間伝達関数を出力します。

Transfer function:
         0.01187 z^2 + 0.06408 z + 0.009721
z^(-2) * ----------------------------------
             z^3 - 1.655 z^2 + 0.7408 z
 
Sampling time: 0.1

ここで、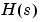 の中の入力遅れは、サンプリング周期0.1秒の2.5倍と見積もられます。従って、離散化モデルhdは、hd.inputdelayの値により確認できるように、2サンプリング周期の入力遅れを継承しています。サンプリング周期より小さい遅れは、離散化アルゴリズムによってhdの係数の中に含ませています。

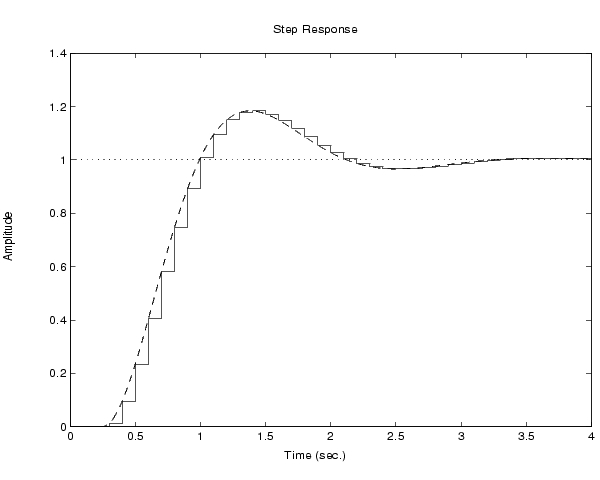
連続モデルと離散モデルのステップ応答を、つぎの図に示しています。このプロットは、つぎのコマンドで作成できます。

step(h,'--',hd,'-')

注意    Tustin法と極/零点マッチング法は、サンプル周期の整数倍の遅れに対してのみ正確です。そのため、遅れを含むモデルに対する離散化手法には、zohやfoh を使うことをお勧めします。

極と零点のマッチング法

離散時間モデルのリサンプリング