Getting Started

SISO例題：DCモータ

慣性負荷を駆動する簡単なDCモータは、入力として供給電圧vapp(t)、出力として負荷の角度比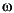(t)をもっています。この例題の目的は、適用する電圧の変化により、角度比を制御することです。つぎの図は、簡単なDCモータを示しています。

図 2-1：慣性負荷を駆動するDCモータの簡単なモデル

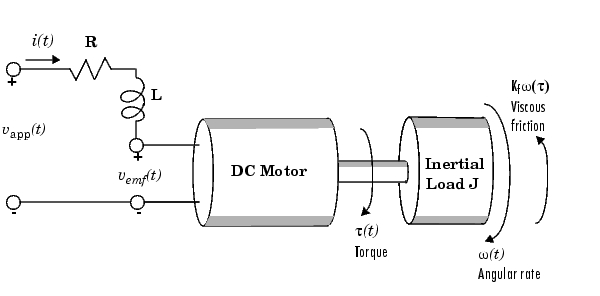
このモデルで、モータ自身のダイナミックスが理想化されています。たとえば、磁場は一定と考えられています。回路の抵抗をRとし、電機子の自己インダクタンスをLとします。DCモータのモデル化に詳しくない方は、物理的なモデリングに関する基礎的なテキストを参照してください。ここで、重要な事柄は、簡単なモデルと物理的な基礎法則を使って、電気力学システムの挙動を記述する微分方程式を作成することです。この例題では、電気的なポテンシャルと力学的な力との間の関係は、Faradayの法則と磁場内を移動する導体に作用するAmpèreの法則です。

運動的な導出

モータのシャフトに見られるトルク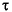 は、適用された電圧で発生する電流iに比例します。

ここで、K₁は電機子の定数で、モータの物理的な特性、たとえば、磁場の強さ、導体コイルの周りを巻いているワイヤの数、等々に関連します。誘電電流による力vemfは、シャフトで見られる角度比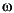に比例した電圧になります。

ここで、K₂は、起電力の定数で、モータの物理特性に依存します。

モータの方程式の力学的な部分は、慣性負荷Jと角度比の微係数を乗算したものが、モータのシャフトの周りの全トルク量に等しいNewtonの法則に従います。結果は、つぎのように表せます。

ここで、K_f は、粘性摩擦の線形近似です。

最終的に、モータの方程式の電気的な部分は、つぎの方程式

で記述でき、または、逆方向の誘電電流を代入して、適用する電圧に対して、つぎの方程式を解きます。

一連の方程式は、モータの挙動を記述した誘電電流を表す

と、結果求まる角度比

DCモータに対する状態空間方程式

前の節で導出した2つの微分方程式を与えて、ダイナミックシステムとして、DCモータの状態空間表現を作成することができます。電流i と角度比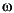は、システムの2つの状態です。適用される電圧vappは、システムへの入力で、角度比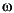は、出力になります。

図2-2：DCモータの例題の状態空間表現

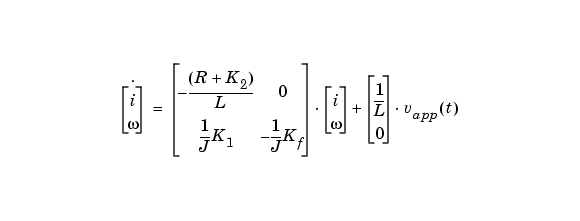
線形モデルの表現

SISOモデルの構築