| 設計ケーススタディ | |
x軸に対するLQG設計
最初の近似として、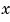
-軸と
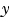-軸間の相互干渉を無視し、各軸を独立に扱います。すなわち、各軸に対して、1つのSISO LQGレギュレータを設計します。設計目標は、偏心と入力外乱による厚さの変動
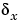と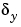
を抑えることです。
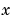-軸から開始します。まず、モデル構成要素を伝達関数オブジェクトとして設定します。
% 油圧アクチュエータ(入力は'u-x') Hx = tf(2.4e8,[1 72 90^2],'inputname','u-x') % 入力の厚さ/硬さ外乱モデル Fix = tf(1e4,[1 0.05],'inputn','w-ix') % 圧延偏心モデル Fex = tf([3e4 0],[1 0.125 6^2],'inputn','w-ex') % 力から厚さギャップへのゲイン gx = 1e-6;
つぎに、図1-1に示した開ループモデルを作成します。この目的のために関数connectを利用することができますが、このモデルは、基本的なappendおよびseries結合で作成する方が簡単です。
% 入力から力f1、f2へのI/O射影
Px = append([ss(Hx) Fex],Fix)
% f1、f2から出力'x-gap'および'x-force'への静的ゲインを追加
Px = [-gx gx;1 1] * Px
% 出力名称を付ける
set(Px,'outputn',{'x-gap' 'x-force'})
ここで、変数Pxは、入力名と出力名をもった開ループ状態空間モデルで含んでいます。
Px.inputname
ans =
'u-x'
'w-ex'
'w-ix'
Px.outputname
ans =
'x-gap'
'x-force'
第2出力'x-force'は、圧延力の測定値です。LQGレギュレータは、この測定値を用いて、油圧アクチュエータを駆動し、外乱による厚さの変動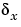
を抑えます。
'x-force'を与えて、状態ベクトルを推定するKalmanフィルタを設計します。
評価関数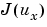
は、低周波数にとっても、高周波数にとっても不利です。低周波数変動が第一の関心事なので、ローパスフィルタ
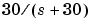を用いて、
の高周波成分を除去し、LQ評価関数にフィルタ処理した値を使用します。
lpf = tf(30,[1 30])
% ローパスフィルタをPxの第一出力に結合する
Pxdes = append(lpf,1) * Px
set(Pxdes,'outputn',{'x-gap*' 'x-force'})
% LQRYおよびq=1,r=1e-4を用いて状態フィードバックゲインを設計する
kx = lqry(Pxdes(1,1),1,1e-4)
注意：
lqryは、すべての入力が指令値であり、すべての出力が観測値であると仮定します。ここで、指令値'u-x'および観測値'x-gap*'(フィルタ処理したギャップ)は、Pxdesの第1入力と第1出力です。従って、構文Pxdes(1,1)を用いて、'u-x'と'x-gap*'のI/O関係のみを設定します。 |
つぎに、関数kalmanを用いて、Kalman状態推定器を設計します。プロセスノイズ
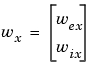
は、構造上単位共分散をもっています。観測ノイズ共分散を1000に設定して、高周波数ゲインを制限し、推定器設計用に測定した出力'x-force'のみを観測量とします。
estx = kalman(Pxdes(2,:),eye(2),1000)
最後に、状態フィードバックゲインkxと状態推定器estxを結合して、LQGレギュレータを構成します。
Regx = lqgreg(estx,kx)
ここで、0.1-1000ラジアン/秒の範囲でレギュレータBode線図を見てみます。
-軸用のLQG設計は完了します。
bode(Regx,{0.1 1000})
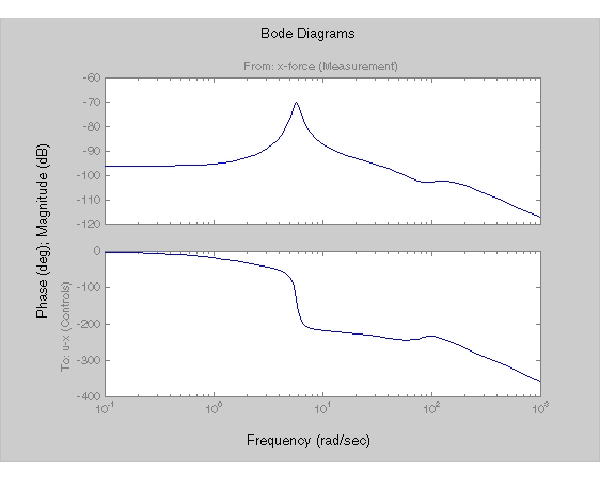
位相応答については、興味深い物理解釈ができます。まず、入力の厚さの増加を考えます。この低周波数外乱は、出力の厚さと圧延力のいずれをも高めます。レギュレータ位相は、低周波数で約0度なので、油圧力を増加することによって、フィードバックループは適切に反応し、厚さの増加を相殺します。ここで、偏心の影響について考慮します。偏心は、圧延ギャップ(圧延シリンダ間のギャップ)の変動の原因となります。圧延ギャップが最小のとき、圧延力は増加し、ビームの厚さは減少します。この場合には、油圧力を減少させて(負の力のフィードバック)、希望する厚さに戻す必要があります。これは、まさに偏心外乱(6 ラジアン/秒)の固有周波数近辺で位相が-180度まで遅れるときに、LQGレギュレータが実行することに他なりません。
つぎに、外乱から厚さギャップへの開ループ応答と閉ループ応答とを比較します。feedbackを用いてループを閉じます。フィードバック結合の設定を容易にするには、プラントPxとレギュレータRegxのI/O名前を参照します。
Px.inputname
ans =
'u-x'
'w-ex'
'w-ix'
Regx.outputname
ans =
'u-x'
Px.outputname
ans =
'x-gap'
'x-force'
Regx.inputname
ans =
'x-force'
このことは、Pxの第1入力と第2出力をレギュレータに結合しなければならないことを意味します。
clx = feedback(Px,Regx,1,2,+1) % 注意：正のフィードバックに対しては+1
これで、外乱から厚さギャップへの開ループBode線図と閉ループBode線図との比較を行う準備ができました。
bode(Px(1,2:3),'--',clx(1,2:3),'-',{0.1 100})
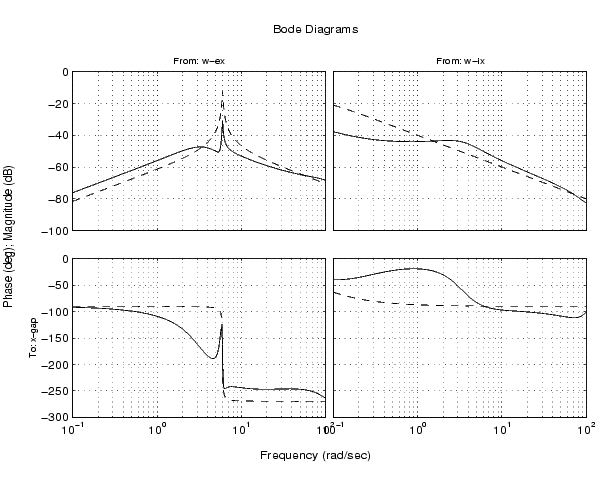
破線は、開ループ応答を示しています。偏心からギャップへの応答のピークゲインと入力の厚さからギャップへの応答の低周波数ゲインが、約20dB減少したことに注目してください。
最後に、lsimを用いて白色ノイズ入力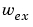
と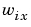
に対する開ループおよび閉ループの時間応答をシミュレーションします。シミュレーションのサンプリング周期として、dt=0.01を選択し、このサンプリングレートに対する等価離散白色ノイズ入力を導きます。
dt = 0.01 t = 0:dt:50 % 時間サンプル % 単位共分散の励起ノイズwx =[w-ex;w-ix]を生成 % 等価離散共分散は1/dt wx = sqrt(1/dt) * randn(2,length(t)) lsim(Px(1,2:3),':',clx(1,2:3),'-',wx,t)
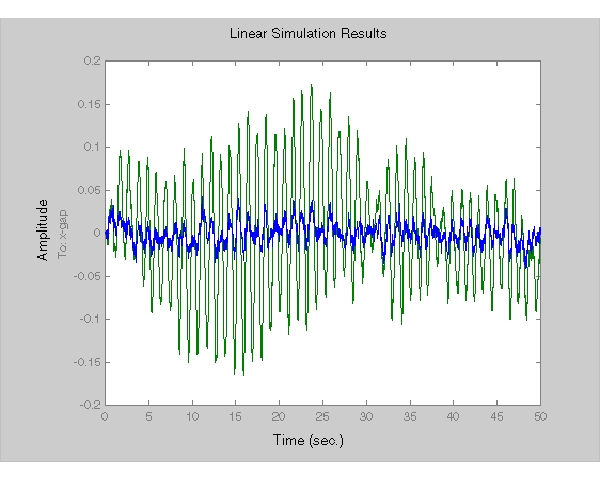
点線は、開ループ応答に対応します。このシミュレーションでは、LQGレギュレータにより、厚さの変動がピークの4分の1に抑えられます。
| | プロセスと外乱モデル | y軸に対するLQG設計 | |