設計ケーススタディ

ハードディスク読み書きヘッドコントローラ

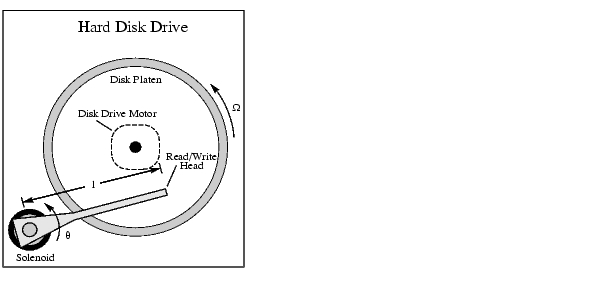
このケーススタディは、コンピュータハードディスクの読み書きヘッド位置制御系設計を通して、古典的デジタル制御設計を実行する機能を実証するものです。

Newtonの法則により、読み書きヘッドの単純なモデルは、つぎの微分方程式で表されます。

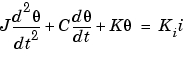
ここで、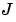はヘッドアセンブリの慣性、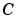はベアリングの粘性減衰係数、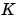は戻しバネ定数、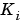はモータトルク定数、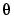はヘッドの角位置、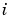は入力電流です。

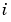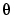Laplace変換を用いると、からへの伝達関数は、つぎのようになります。

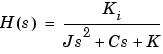
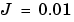Kg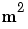 、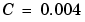Nm/(rad/sec)、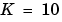Nm/rad、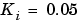Nm/radの各値を用いると、このシステムの伝達関数の記述は、つぎのようになります。

J = .01; C = 0.004; K = 10; Ki = .05;
num = Ki;
den = [J C K];
H = tf(num,den)

MATLABは、つぎの出力を行います。

Transfer function:
         0.05
-----------------------
0.01 s^2 + 0.004 s + 10

ここで行うべきことは、読み書きヘッドの正確な位置決めを行うデジタルコントローラを設計することです。設計は、離散領域で行われます。まず、連続プラントを離散化します。このプラントは、その入力に接続されたデジタル-アナログ変換器(ゼロ次ホールド付き)を搭載しているので、'zoh'離散化法で、c2dを使用します。

Ts = 0.005;     % サンプリング周期=0.005 秒
Hd = c2d(H,Ts,'zoh')

Transfer function:
6.233e-05 z + 6.229e-05
-----------------------
 z^2 - 1.973 z + 0.998
 
Sampling time: 0.005

つぎのようにして、連続、離散モデルのBode線図を比較することができます。

bode(H,'-',Hd,'--')

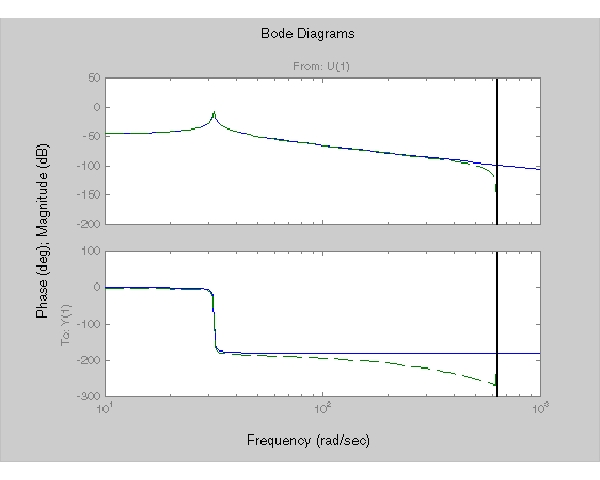
離散システムを分析するには、そのステップ応答をつぎのようにプロットします。

step(Hd)

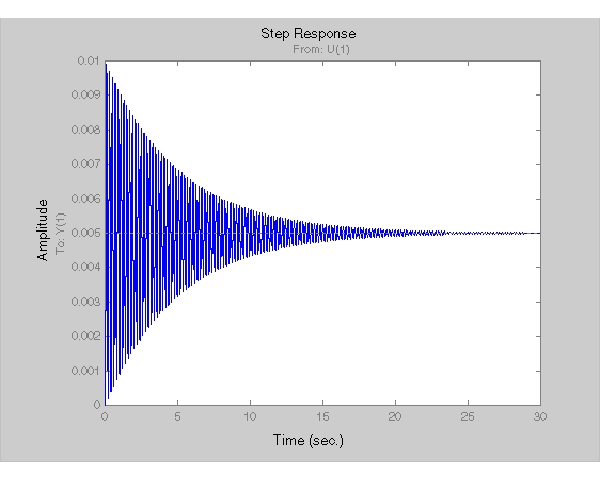
このシステムは、大きな振動を示します。これは、おそらく減衰が非常に小さいためです。これは、開ループの極を計算することによって確認できます。

% 離散モデルの開ループの極
damp(Hd) 

    Eigenvalue         Magnitude    Equiv. Damping    Equiv. Freq.
                                                                               
9.87e-01 + 1.57e-01i     9.99e-01         6.32e-03             3.16e+01        
9.87e-01 - 1.57e-01i     9.99e-01         6.32e-03             3.16e+01        

これらの極は、非常に小さな減衰率をもち、単位円に接近しています。これらの極の減衰を大きくするような補償器を設計する必要があります。

もっとも単純な補償器は単なるゲインですから、根軌跡法を用いて適切なフィードバックゲインを選択します。

rlocus(Hd)

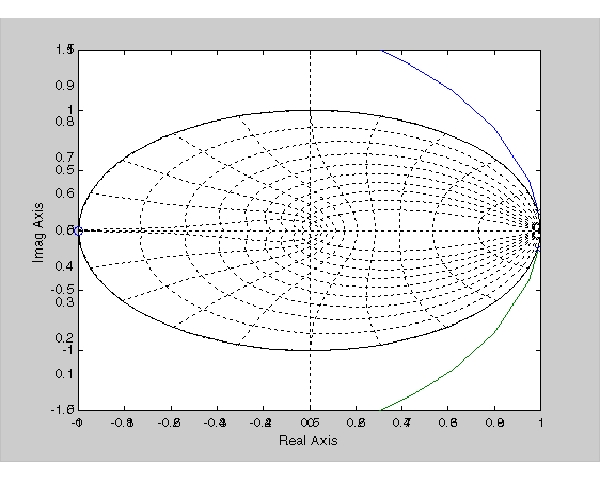
根軌跡で示すように、極は急激に単位円から離れて不安定になります。ある位相進み補償器、または、ある零点をもつ補償器を導入する必要があります。つぎの補償器を設計します。

ここで、、とします。

対応する開ループモデル

は、つぎの直列結合で得られます。

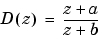
D = zpk(0.85,0,1,Ts)
oloop = Hd * D

ここで、この補償器が開ループ周波数応答をどのように修正するかを確認します。

bode(Hd,'--',oloop,'-')

プラント応答は破線で示し、補償器をもつ開ループ応答は実線で示します。

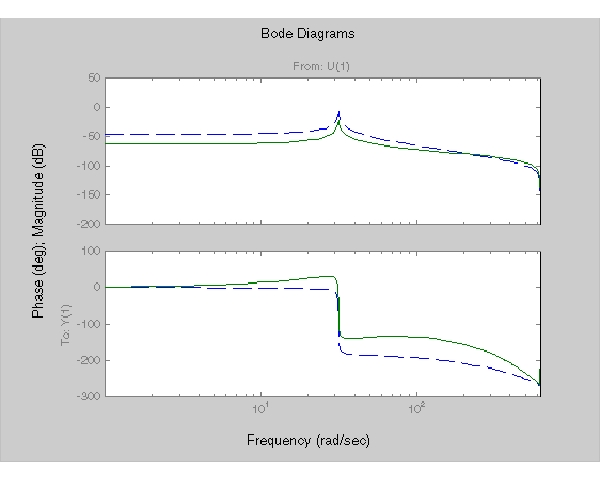
上のプロットでは、補償器が周波数範囲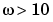ラジアン/秒で、位相プロットを(付加した位相進み特性だけ)上方へシフトしていることがわかります。

ここで、このプラントと補償器の直列結合に対する根軌跡を示します。

rlocus(oloop)
zgrid

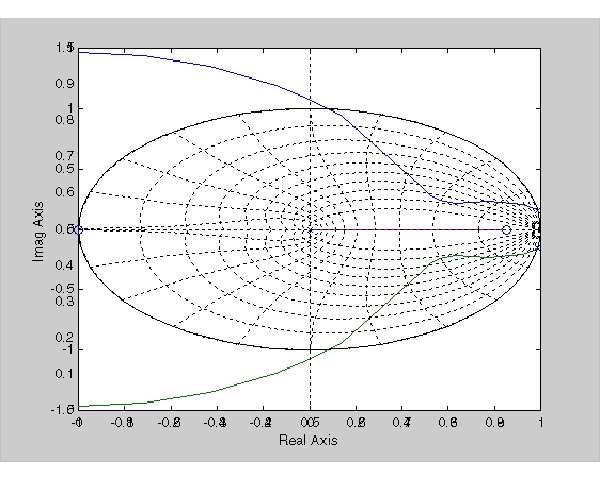
この場合、極がある程度の間、単位円内に留まります(zgridで描かれた線は、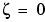から1までの減衰率を0.1の間隔で示します)。このプロットは、つぎのrlocfindを用いて、選択した極'+'の集合を示します。MATLABプロンプトのもとで、つぎのように入力します。

[k,poles] = rlocfind(oloop)

k
k =
   4.1179e+03

つぎのようにタイプしてください。

ddamp(poles,Ts)

は、それぞれの固有値に対する等価な減衰係数と固有周波数を出力します。

この設計を解析するためには、閉ループシステムを構成して、閉ループステップ応答をプロットします。

cloop = feedback(oloop,k);
step(cloop)

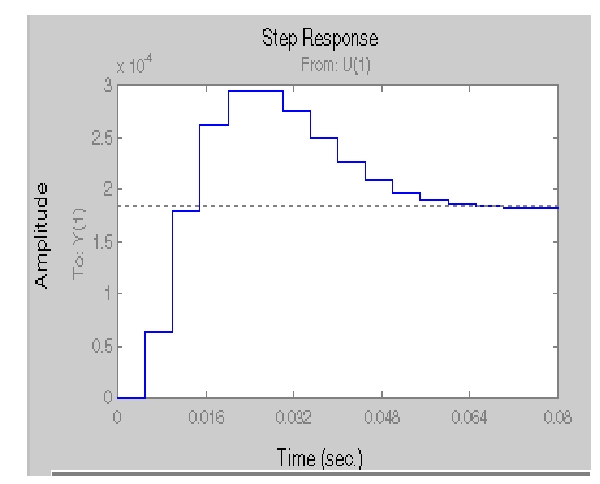
この応答は、ユーザの閉ループセットポイントに依存しています。ここで示すものは、比較的速く、約0.07秒で落ち着きます。そのため、この閉ループディスクシステムは、約0.07秒のシーク時間をもっています。これは、今日の基準では遅いものですが、それは非常に軽い減衰システムから開始したためでもあります。

ここで、この設計のロバスト性を考えてみます。最も一般的な古典的ロバスト性の基準は、ゲイン余裕と位相余裕です。関数marginを用いて、これらの余裕を決定します。出力引数により、marginはゲイン余裕と位相余裕、および対応するクロスオーバ周波数を出力します。出力引数が設定されていない場合、marginは、Bode線図をプロットし、これらの余裕をグラフに示します。

余裕を計算するには、まず、補償器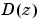、プラントモデル、フィードバックゲイン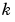を直列に結合することによって単一フィードバック開ループを構成します。

olk = k * oloop;

つぎに、marginをこの開ループモデルに適用します。つぎのようにタイプインしてください。

[Gm,Pm,Wcg,Wcp] = margin(olk);
Margins = [Gm Wcg Pm Wcp]

Margins =
    3.7809  295.3172   43.1686  106.4086

デシベル表示にするには、つぎのように入力してください。

20*log10(Gm)
ans =
   11.5760

margin(olk)

このコマンドによって、つぎの線図が表示されます。

この設計は、ロバストで、不安定になるまでに11dBのゲインの増加、または、40度の位相の遅れを許容します。この設計のプロセスを継続することによって、開ループシステムを安定化し、シーク時間を短縮することができる補償器を見つけることができます。

washoutフィルタ設計

LQGレギュレータ