設計ケーススタディ (Design Case Studies)

設計ケーススタディ

根軌跡法による設計

最も簡単な補償器は静的ゲインなので、まず根軌跡法を用いて適切なゲインの値を決定します。

% (1,1)チャンネルに対する根軌跡をプロット
rlocus(sys11)

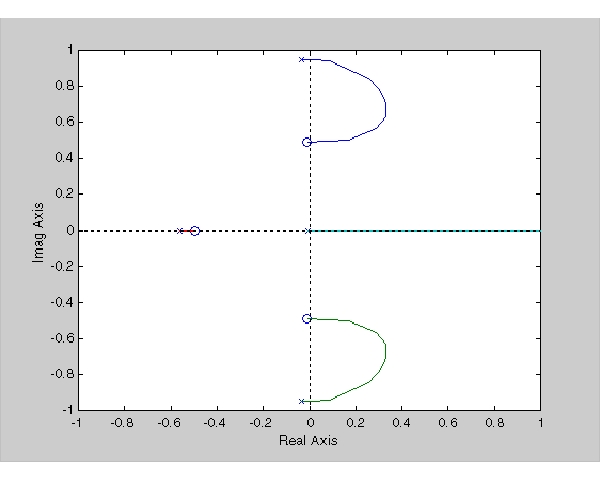
これは、負のフィードバックに対する根軌跡で、システムがほぼ瞬間的に不安定になることを示しています。その代わりに、正のフィードバックを用いるとシステムの安定性を維持することができます。

rlocus(-sys11)
sgrid

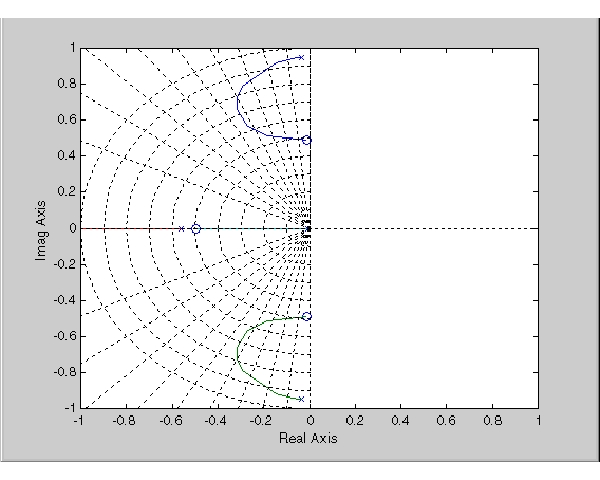
このほうが、良いように思われます。単純なフィードバックを用いるだけで、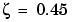の減衰率を達成することができます。グラフ上で、いくつかの極の位置を選択し、rlocfindで対応するゲインを決定することができます。

[k,poles] = rlocfind(-sys11)

上図の'+'マークは、選択可能な状態を示しています。対応するゲインと閉ループの極は、つぎのとおりです。

k
 
k =
    2.7615
 
damp(poles)
                                                         
        Eigenvalue            Damping     Freq. (rad/s)  
                                                         
 -1.01e+000                  1.00e+000      1.01e+000    
 -3.03e-001 + 6.18e-001i     4.41e-001      6.89e-001    
 -3.03e-001 - 6.18e-001i     4.41e-001      6.89e-001    
 -3.33e-001                  1.00e+000      3.33e-001

つぎに、この設計を解析できるように閉ループシステムを構成します。

cl11 = feedback(sys11,-k);   % デフォルトでは負のフィードバック

閉ループ極は、上で選択した極と一致しなければなりません(実際一致します)。

damp(cl11)

        Eigenvalue            Damping     Freq. (rad/s)  
                                                         
 -3.33e-001                  1.00e+000      3.33e-001    
 -3.03e-001 + 6.18e-001i     4.41e-001      6.89e-001    
 -3.03e-001 - 6.18e-001i     4.41e-001      6.89e-001    
 -1.01e+000                  1.00e+000      1.01e+000

20秒間だけ閉ループのインパルス応答をプロットします。

impulse(cl11,20)

その応答は、直ちに安定になり、あまり振動しません。

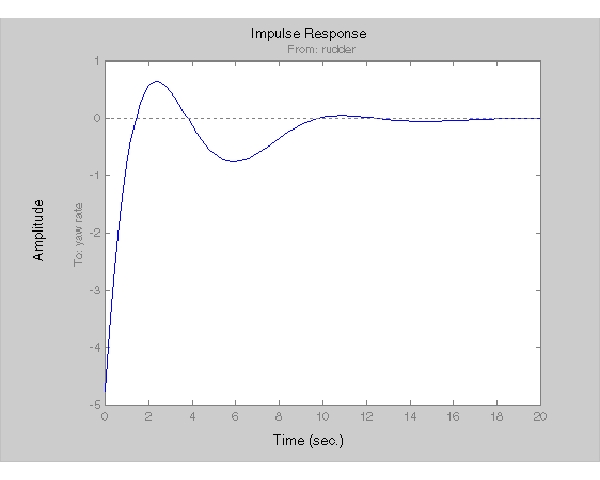
ここで、最初のモデルのループを閉じて、補助翼からの応答がどのようになるかを確認します。フィードバックループには、プラントの入力1と出力1が含まれています(この入力/出力ペアを選択するインデックスベクトルを入力引数として、feedbackを使用します)。MATLABで、つぎのように入力します。

cloop = feedback(sys,-k,1,1);
damp(cloop)    % 閉ループの極

MATLABは、つぎの出力を行います。

                                                   
        Eigenvalue            Damping     Freq. (rad/s)  
                                                         
 -3.33e-001                  1.00e+000      3.33e-001    
 -3.03e-001 + 6.18e-001i     4.41e-001      6.89e-001    
 -3.03e-001 - 6.18e-001i     4.41e-001      6.89e-001    
 -1.01e+000                  1.00e+000      1.01e+000

MIMO インパルス応答をプロットします。

impulse(cloop,20)

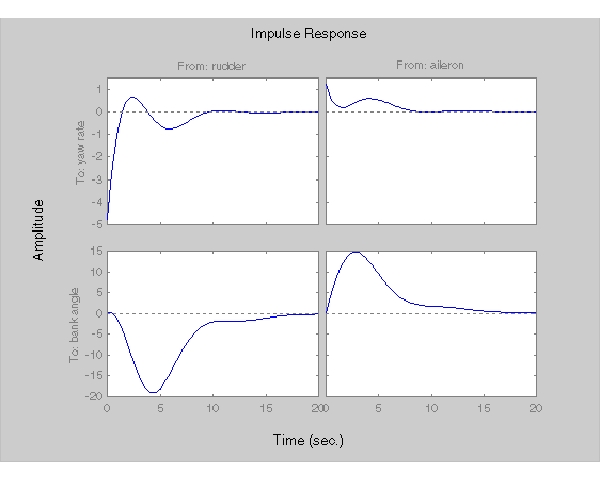
補助翼(入力2)からバンク角(出力2)への応答を見てください。補助翼をインパスル的に操作しても、制御をしていない通常の飛行機とは異なり、バンク角が元に戻っています。これは、スパイラルモードを過度に安定化したことになります。通常は、スパイラルモードは非常に遅いので、補助翼を操作し続けなくても、機体を傾けながら旋回を行うことができます。パイロットは、このような操作に慣れているので、このような操作ができないスパイラルモードを過度に安定化したこの設計は好みません。そこで、スパイラルモードを高周波数側に移動することにします。

開ループ解析 washoutフィルタ設計