

| 設計ケーススタディ |   |
定常状態の設計
関数kalmanを用いて、上記の定常状態Kalmanフィルタを設計することができます。まず、つぎのプロセスノイズをもつプラントモデルを設定します。
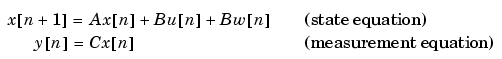
% 注意:サンプル時間を-1に設定することにより、モデルが離散系であることを示す。
Plant = ss(A,[B B],C,0,-1,'inputname',{'u' 'w'},...
'outputname','y');
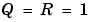 と仮定すると、以下の方法で離散Kalmanフィルタを設計することができます。
と仮定すると、以下の方法で離散Kalmanフィルタを設計することができます。
Q = 1; R = 1; [kalmf,L,P,M] = kalman(Plant,Q,R);
これは、フィルタの状態空間モデルkalmfとイノベーションゲインMを出力します。
M M = 3.7980e-01 8.1732e-02 -2.5704e-01
kalmfの入力は、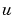 および
および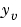 で、その出力は、プラント出力、および、つぎの状態推定値です(
で、その出力は、プラント出力、および、つぎの状態推定値です(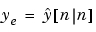 と
と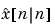 )。
)。
ここで、関心があるのは出力推定値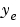 なので、つぎの
なので、つぎのkalmfの第1出力のみを抜き出します。
kalmf = kalmf(1,:);MATLABは、つぎの出力を行います。
kalmf
a =
x1_e x2_e x3_e
x1_e 0.76830 -0.49400 0.11290
x2_e 0.62020 0 0
x3_e -0.08173 1.00000 0
b =
u y
x1_e -0.38320 0.35860
x2_e 0.59190 0.37980
x3_e 0.51910 0.08173
c =
x1_e x2_e x3_e
y_e 0.62020 0 0
d =
u y
y_e 0 0.37980
Sampling time: unspecified
Discrete-time system.
フィルタが、どのように機能するかを見るためには、何らかの入力データとランダムノイズを生成し、フィルタを適用した応答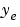 と真の応答
と真の応答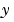 を比較します。それぞれの応答は、別々に生成することも、同時に生成することもできます。それぞれの応答を別々にシミュレーションするには、まずプラントだけで
を比較します。それぞれの応答は、別々に生成することも、同時に生成することもできます。それぞれの応答を別々にシミュレーションするには、まずプラントだけでlsimを使用し、ついでプラントとフィルタを一緒にして、lsimを使用します。両者を同時にシミュレーションする、もう1つの方法については、つぎに説明します。
下のブロックダイアグラムは、真の出力とフィルタを適用した出力を生成する方法を示したものです。
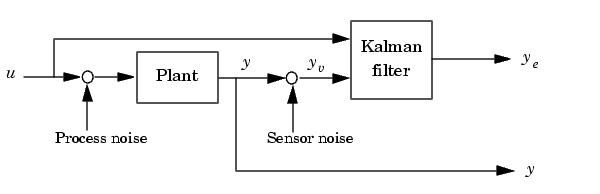
このブロックダイアグラムの状態空間モデルは、関数parallelとfeedbackを用いて設計することができます。まず、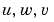 を入力とし、
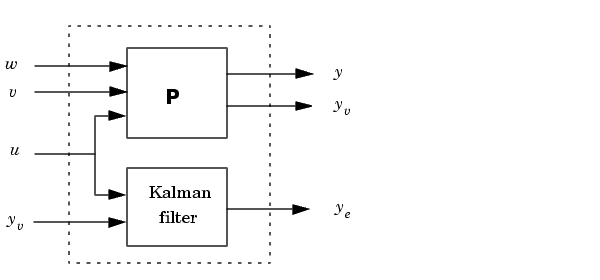
を入力とし、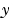 と
と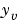 (測定値)を出力とする完全なプラントモデルを作成します。
(測定値)を出力とする完全なプラントモデルを作成します。
a = A;
b = [B B 0*B];
c = [C;C];
d = [0 0 0;0 0 1];
P = ss(a,b,c,d,-1,'inputname',{'u' 'w' 'v'},...
'outputname',{'y' 'yv'});
つぎに、parallelを用いて、つぎの並列結合を作成します。
sys = parallel(P,kalmf,1,1,[],[])
最後に、プラント出力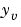 を正のフィードバックで、フィルタ入力
を正のフィードバックで、フィルタ入力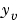 に結合することによってセンサループを閉じます。
に結合することによってセンサループを閉じます。
% 入力#4と出力#2に関してループを閉じる SimModel = feedback(sys,1,4,2,1) % I/Oリストからyvを削除する SimModel = SimModel([1 3],[1 2 3])
結果として得られるシミュレーションモデルは、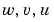 を入力とし、
を入力とし、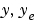 を出力とします。
を出力とします。
SimModel.input
ans =
'w'
'v'
'u'
SimModel.output
ans =
'y'
'y_e'
これで、フィルタの挙動をシミュレーションする準備ができました。正弦波入力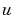 、プロセスノイズベクトル
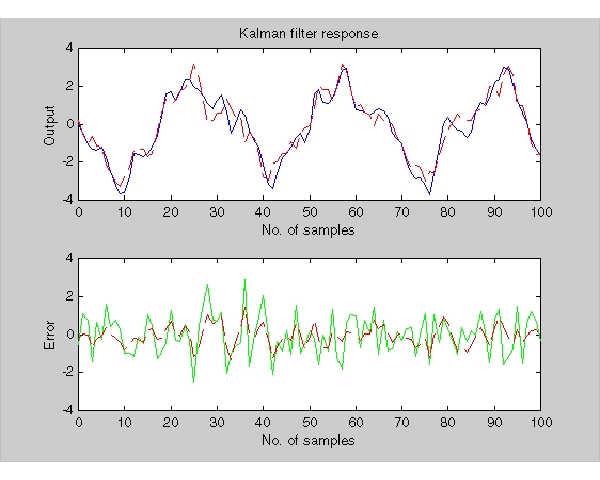
、プロセスノイズベクトル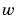 、測定ノイズベクトル
、測定ノイズベクトル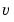 を生成します。
を生成します。
t = [0:100]';
u = sin(t/5);
n = length(t)
randn('seed',0)
w = sqrt(Q)*randn(n,1);
v = sqrt(R)*randn(n,1);
[out,x] = lsim(SimModel,[w,v,u]); y = out(:,1); % 真の応答 ye = out(:,2); % フィルタを適用した応答 yv = y + v; % 観測した応答
また、真の応答とフィルタを適用した応答をグラフ上で比較します。
subplot(211), plot(t,y,'--',t,ye,'-'),
xlabel('No. of samples'), ylabel('Output')
subplot(212), plot(t,y-yv,'-.',t,y-ye,'-'),
xlabel('No. of samples'), ylabel('Error')
最初のプロットは、真の応答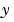 (破線)とフィルタを適用した出力
(破線)とフィルタを適用した出力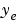 (実線)を示しています。第2のプロットは、測定誤差(鎖線と点)と推定誤差(実線)を比較しています。このプロットは、ノイズレベルが著しく減少したことを示しています。これは、つぎの誤差共分散の計算で確認されます。
(実線)を示しています。第2のプロットは、測定誤差(鎖線と点)と推定誤差(実線)を比較しています。このプロットは、ノイズレベルが著しく減少したことを示しています。これは、つぎの誤差共分散の計算で確認されます。
MeasErr = y-yv; MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr); EstErr = y-ye; EstErrCov = sum(EstErr.*EstErr)/length(EstErr);
フィルタ処理を行う前の誤差共分散(測定誤差)は、つぎのとおりです。
MeasErrCov
MeasErrCov =
1.1138
一方、フィルタ処理を行った後の誤差共分散(推定誤差)は、つぎのとおりです。
EstErrCov
EstErrCov =
0.2722
 | 離散Kalmanフィルタ | 時変Kalmanフィルタ |  |