設計ケーススタディ

MIMO LQG設計

導いた完全な2軸状態空間モデルPcから開始します。モデルの入力、出力は、つぎのとおりです。

Pc.inputname

ans = 
    'u-x'
    'u-y'
    'w-ex'
    'w-ix'
    'w_ey'
    'w_iy'

P.outputname

ans = 
    'x-gap'
    'y-gap'
    'x-force'
    'y-force'

前と同様、'x-gap'と'y-gap'の出力に直列にローパスフィルタを結合し、低周波数の厚さ変動のみを抑制します。

Pdes = append(lpf,lpf,eye(2)) * Pc
Pdes.outputn = Pc.outputn

つぎに、前と同様、LQゲインと状態推定器を設計します(ここには、2つの指令値と2つの観測値があります)。

k = lqry(Pdes(1:2,1:2),eye(2),1e-4*eye(2))     % LQゲイン
est = kalman(Pdes(3:4,:),eye(4),1e3*eye(2))    % Kalman推定器

RegMIMO = lqgreg(est,k)    % MIMO LQGレギュレータを作成

結果として得られるLQGレギュレータRegMIMOには、2つの入力と2つの出力があります。

RegMIMO.inputname

ans = 
    'x-force'
    'y-force'

RegMIMO.outputname

ans = 
    'u-x'
    'u-y'

その特異値応答(主ゲイン)をプロットします。

sigma(RegMIMO)

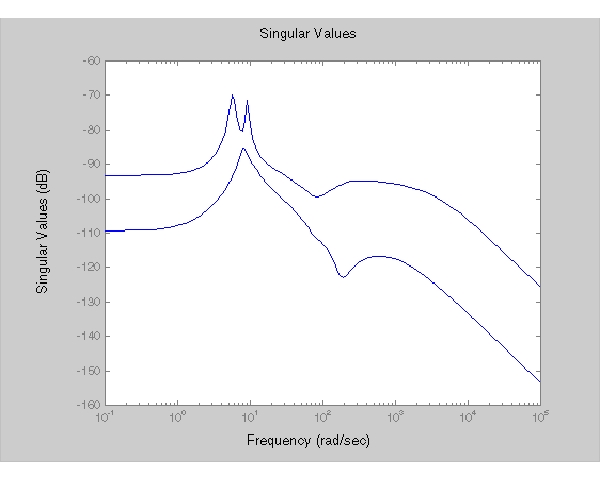
つぎに、(フィードバックに対するMIMO LQGレギュレータを用いて)白色ノイズ入力に対する開ループ時間応答と閉ループ時間応答をプロットします。

% 閉ループモデルを作成
cl = feedback(Pc,RegMIMO,1:2,3:4,+1);

% 同じノイズ入力を用いたLSIM でのシミュレーション
lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)

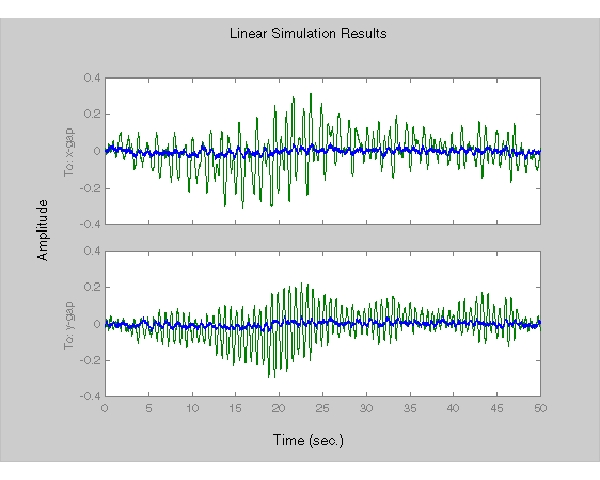
MIMO設計は、各軸に対する独立のSISO設計より明らかに改良されています。特に、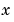/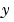軸の厚さ変動のレベルは、分離したケースで得られるレベルに匹敵するものです。この例題は、多変数システムに対するMIMO設計の利点を示しています。

軸同士の相互干渉

Kalmanフィルタ処理